
分析 (1)根据*的含义,以及有理数的混合运算的运算方法,求出2*5的值是多少即可.
(2)根据*的含义,以及有理数的混合运算的运算方法,求出(1*3)*(-4)的值是多少即可.
(3)首先根据*的含义,以及有理数的混合运算的运算方法,求出a*(b+c)与a*b+a*c的值各是多少;然后用等式将其表达出来即可.
解答 解:(1)-2*5=-2×5+2=-8
(2)(1*3)*(-4)
=(1×3+2)*(-4)
=5*(-4)
=5×(-4)+2
=-18
(3)a*(b+c)
=a(b+c)+2
=ab+ac+2
a*b+a*c
=ab+2+ac+2
=ab+ac+4
∴a*(b+c)+2=a*b+a*c.
点评 此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
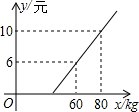 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
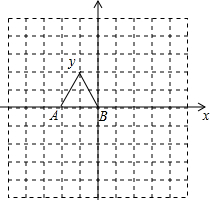 如图,在边长均为1的小正方形网格纸中,△OAB的顶点0、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
如图,在边长均为1的小正方形网格纸中,△OAB的顶点0、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,且∠BAO=30°,现将△OAB沿直线AB翻折,得到△CAB.连接OC交AB于点D.
如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,且∠BAO=30°,现将△OAB沿直线AB翻折,得到△CAB.连接OC交AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com