
【题目】请将下列证明过程补充完整:
已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
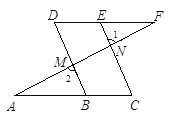
求证:∠C=∠D.
证明:因为∠1=∠2(已知),
又因为∠1=∠ANC( ),
所以 (等量代换).
所以 ∥ (同位角相等,两直线平行),
所以∠ABD=∠C( ).
又因为∠A=∠F(已知),
所以 ∥ ( ).
所以 (两直线平行,内错角相等).
所以∠C=∠D( ).
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
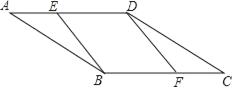
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地后立即以另一速度按原路匀速返回到
地后立即以另一速度按原路匀速返回到![]() 地; 乙车匀速前往
地; 乙车匀速前往![]() 地,设甲、乙两车距
地,设甲、乙两车距![]() 地的路程为
地的路程为![]() (千米),甲车行驶的时间为
(千米),甲车行驶的时间为![]() 时),
时), ![]() 与
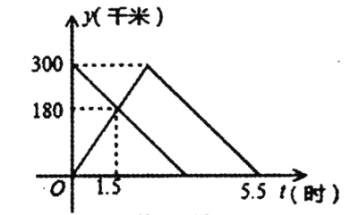
与![]() 之间的函数图象如图所示
之间的函数图象如图所示
(1)甲车从![]() 地到
地到![]() 地的速度是__________千米/时,乙车的速度是__________千米/时;
地的速度是__________千米/时,乙车的速度是__________千米/时;
(2)求甲车从![]() 地到达
地到达![]() 地的行驶时间;
地的行驶时间;
(3)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(4)求乙车到达![]() 地时甲车距
地时甲车距![]() 地的路程.
地的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
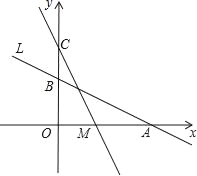
【题目】如图,直线L:y=-![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,a、c满足![]() .AB表示点A、B之间的距离,且
.AB表示点A、B之间的距离,且![]() .
.
![]()
(1)![]() ________,
________,![]() ________;
________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数________表示的点重合;
(3)点A、B、C在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则![]() ________,
________,![]() ________.(用含t的代数式表示)
________.(用含t的代数式表示)
(4)在(3)的条件下,请问:![]() 的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
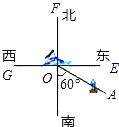
(1)仿照表示灯塔方位的方法,分别画出表示客轮B和海岛C方向的射线OB、OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,求出∠AOD的度数;
(3)画出表示渔船D方向的射线OD,则渔船D在货轮O的 (写出方位角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
……
根据上述等式的规律,解答下列问题:
(1)写出第5个等式:________________;
(2)写出第![]() 个等式:__________________(用含有
个等式:__________________(用含有![]() 的代数式表示);
的代数式表示);
(3)应用你发现的规律,计算:![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索代数式a2![]() 2ab+b2与代数式(a
2ab+b2与代数式(a ![]() b)2的关系.
b)2的关系.
(1)当a=1,b=2时分别计算两个代数式的值.
(2)当a=3,b= ![]() 2时分别计算两个代数式的值.
2时分别计算两个代数式的值.
(3)你发现了什么规律?
(4)利用你发现的规律计算:732![]() 2×73×67+672.
2×73×67+672.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com