
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地后立即以另一速度按原路匀速返回到
地后立即以另一速度按原路匀速返回到![]() 地; 乙车匀速前往
地; 乙车匀速前往![]() 地,设甲、乙两车距
地,设甲、乙两车距![]() 地的路程为
地的路程为![]() (千米),甲车行驶的时间为
(千米),甲车行驶的时间为![]() 时),
时), ![]() 与
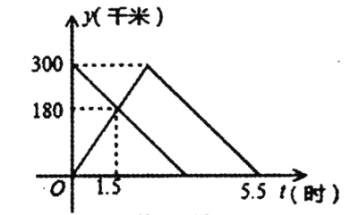
与![]() 之间的函数图象如图所示
之间的函数图象如图所示
(1)甲车从![]() 地到
地到![]() 地的速度是__________千米/时,乙车的速度是__________千米/时;
地的速度是__________千米/时,乙车的速度是__________千米/时;
(2)求甲车从![]() 地到达
地到达![]() 地的行驶时间;
地的行驶时间;
(3)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(4)求乙车到达![]() 地时甲车距
地时甲车距![]() 地的路程.
地的路程.
【答案】(1)![]() ;
;
(2)甲车从![]() 地到达
地到达![]() 地的行驶时间是2.5小时;
地的行驶时间是2.5小时;
(3)甲车返回时![]() 与
与![]() 之间的函数关系式是
之间的函数关系式是![]() ;
;
(4)乙车到达![]() 地时甲车距
地时甲车距![]() 地的路程是175千米.
地的路程是175千米.
【解析】
(1)根据题意列算式计算即可得到结论;
(2)根据题意列算式计算即可得到结论;
(3)设甲车返回时![]() 与
与![]() 之间的函数关系式为y=kt+b,根据题意列方程组求解即可得到结论;
之间的函数关系式为y=kt+b,根据题意列方程组求解即可得到结论;
(4)根据题意列算式计算即可得到结论.
解:(1)甲车从A地开往B地时的速度是:180÷1.5=120千米/时,乙车从B地开往A地的速度是:(300-180)÷1.5=80千米/时,
故答案为:120;80;
(2)![]() (小时)
(小时)
答:甲车从![]() 地到达
地到达![]() 地的行驶时间是2.5小时
地的行驶时间是2.5小时
(3)设甲车返回时![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ,
,
则有![]()
解得:![]() ,
,
∴甲车返回时![]() 与
与![]() 之间的函数关系式是
之间的函数关系式是![]()
(4)![]() 小时,
小时,
把![]() 代入
代入![]() 得:
得:![]()
答:乙车到达![]() 地时甲车距
地时甲车距![]() 地的路程是175千米.
地的路程是175千米.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
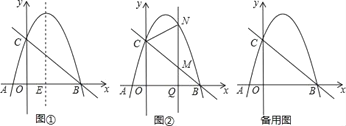
【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
(1)当![]() 时,某用户一个月用了
时,某用户一个月用了![]() 水,求该用户这个月应缴纳的水费;
水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为![]() 立方米,当
立方米,当![]() 时,求该用户应缴纳的水费(用含
时,求该用户应缴纳的水费(用含![]() 、
、![]() 的整式表示);
的整式表示);
(3)当![]() 时,甲、乙两用户一个月共用水
时,甲、乙两用户一个月共用水![]() .已知甲用户用水量超过了
.已知甲用户用水量超过了![]() ,设甲用户这个月用水如
,设甲用户这个月用水如,试求甲、乙两用户一个月共缴纳的水费.(用含
![]() 的整式表示)
的整式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示:
1次 | 2次 | 3次 | 4次 | 5次 | |
小明 | 10 | 14 | 13 | 12 | 13 |
小兵 | 11 | 11 | 15 | 14 | 11 |
根据以上信息,解决以下问题:
(1)小明成绩的中位数是__________.
(2)小兵成绩的平均数是__________.
(3)为了比较他俩谁的成绩更稳定,老师利用方差公式计算出小明的方差如下(其中![]() 表示小明的平均成绩);
表示小明的平均成绩);
![]()
请你帮老师求出小兵的方差,并比较谁的成绩更稳定。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
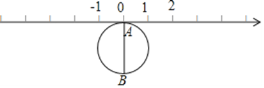
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列证明过程补充完整:
已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
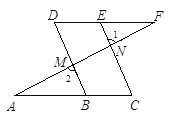
求证:∠C=∠D.
证明:因为∠1=∠2(已知),
又因为∠1=∠ANC( ),
所以 (等量代换).
所以 ∥ (同位角相等,两直线平行),
所以∠ABD=∠C( ).
又因为∠A=∠F(已知),
所以 ∥ ( ).
所以 (两直线平行,内错角相等).
所以∠C=∠D( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转a(0°<a<360°),得到矩形AEFG
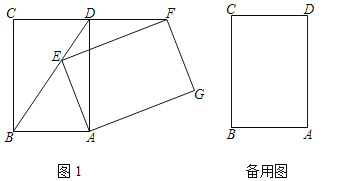
(1)如图1,当点E在BD上时求证:FD=CD;
(2)当a为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com