
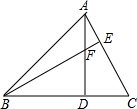
 如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.
如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.
|


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
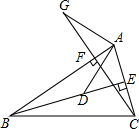 如图,在△ABC中,BE,CF分别是边AC,AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG,则AG与AD有何关系?试给出你的结论的理由.
如图,在△ABC中,BE,CF分别是边AC,AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG,则AG与AD有何关系?试给出你的结论的理由.查看答案和解析>>
科目:初中数学 来源: 题型:
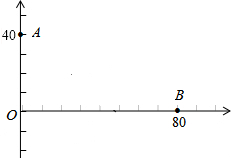 我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标.
我海军某部发现,一艘敌舰从我岛屿O正东方向80海里的B处,沿东西方向向岛屿O驶来,指挥部立即下命令在岛屿O正北40海里A处的我军军舰沿直线前往拦截.若敌我两舰行驶速度相同,在上述坐标系中标出我舰最快截住敌舰的位置,并求出该点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列四个结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列四个结论中:| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在同一个学校上学的小美、小泉、欧欧三位同学住在A、B、C三个住宅小区,如图所示,A、B、C三点共线,且AB=50米,BC=90米.他们打算合租一辆接送车上学(学校位于C的右边),由于车位紧张,准备在此之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点的位置应设在
在同一个学校上学的小美、小泉、欧欧三位同学住在A、B、C三个住宅小区,如图所示,A、B、C三点共线,且AB=50米,BC=90米.他们打算合租一辆接送车上学(学校位于C的右边),由于车位紧张,准备在此之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点的位置应设在查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com