
 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3,则下列判断中正确的是( )
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3,则下列判断中正确的是( )| A. | 此抛物线的解析式为y=x2+x-2 | |
| B. | 当x>0时,y随着x的增大而增大 | |
| C. | 在此抛物线上的某点M,使△MAB的面积等于5,这样的点共有三个 | |
| D. | 此抛物线与直线y=-$\frac{9}{4}$只有一个交点 |
分析 先确定A、B点的坐标,则可利用交点式求出抛物线解析式,于是可对A选项进行判断;根据二次函数的性质对B选项进行判断;设M(t,t2-t-2),根据三角形面积公式得到$\frac{1}{2}$×3×|t2-t-2|=5,再把方程化为t2-t-2=$\frac{10}{3}$或t2-t-2=-$\frac{10}{3}$,然后通过解两个方程确定t的值,从而可对C选项进行判断;通过解方程x2-x-2=-$\frac{9}{4}$可对D选项进行判断.
解答 解:∵CO=2AO,CO=BO,AB=3,
∴OA=1,OB=2,
∴A(-1.0),B(2,0),
∴抛物线解析式为y=(x+1)(x-2),即y=x2-x-2,所以A选项错误;
∵抛物线的对称轴为直线x=$\frac{1}{2}$,
∴当x>$\frac{1}{2}$时,y随着x的增大而增大,所以B选项错误;
设M(t,t2-t-2),
当△MAB的面积等于5,则$\frac{1}{2}$×3×|t2-t-2|=5,
∴t2-t-2=$\frac{10}{3}$或t2-t-2=-$\frac{10}{3}$,
∵方程t2-t-2=$\frac{10}{3}$有两个不等实数解,而方程或t2-t-2=-$\frac{10}{3}$没有实数解,
∴满足条件的M点有2个,所以C选项错误;
当y=-$\frac{9}{4}$时,x2-x-2=-$\frac{9}{4}$,解得x1=x2=$\frac{1}{2}$
∴抛物线与直线y=-$\frac{9}{4}$只有一个交点,所以D选项正确.
故选D.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程.也考查了根的判别式和根与系数的关系.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 | |
| B. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差是S2甲=0.4 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 了解一批电视机的使用寿命,适合用普查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
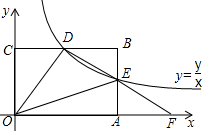 如图,点O是平面直角坐标系的原点,反比例函数y=$\frac{k}{x}$位于第一象限的图象经过矩形ABCO边AB的中点E,与边BC交于点D,连接OD,DE,延长DE与x轴交于点F,则△ODF与矩形ABCO的面积比是$\frac{3}{4}$.
如图,点O是平面直角坐标系的原点,反比例函数y=$\frac{k}{x}$位于第一象限的图象经过矩形ABCO边AB的中点E,与边BC交于点D,连接OD,DE,延长DE与x轴交于点F,则△ODF与矩形ABCO的面积比是$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com