Question

半径为1的⊙O中，两条弦AB=

2

，AC=1，∠BAC的度数为

 

．

Answer 1

考点：垂径定理,解直角三角形

专题：分类讨论

分析：分类讨论：当AC与AB在点A的两旁．由OA=OC=1，AC=1，得到△OAC为等边三角形，则∠OAC=60°，又由OA=OB=1，AB=

2

，得到△OAB为等腰直角三角形，则∠OAB=45°，所以∠BAC=45°+60°=105°；当AC与AB在点A的同旁．有∠BAC=∠OAC-∠OAB=60°-45°=15°．

解答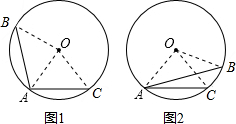：解：如图1，当AC与AB在点A的两旁．
连OC，OA，OB，如图，
在△OAC中，
∵OA=OC=1，AC=1，
∴△OAC为等边三角形，
∴∠OAC=60°；
在△OAB中，
∵OA=OB=1，AB=

2

，即1²+1²=（

2

）²，
∴OA²+OB²=AB²，
∴△OAB为等腰直角三角形，
∴∠OAB=45°，
∴∠BAC=45°+60°=105°；
如图2，当AC与AB在点A的同旁．
同（1）一样，可求得∠OAC=60°，∠OAB=45°，
∴∠BAC=∠OAC-∠OAB=60°-45°=15°．
综上所述：∠BAC的度数为：105°或15°．
故答案为：105°或15°．

点评：本题考查了圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．同时考查了特殊三角形的边角关系和分类讨论的思想的运用．