Question

（本题满分12分）如图，已知抛物线与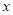轴的一个交点为A（3，0），与轴的交点为B（0，3），其顶点为C，对称轴为．

（1）求抛物线的解析式：

（2）已知点M为y轴上的一个动点，当△ABM为等腰三角形时，求点M的坐标；

（3）将△AOB沿x轴向右平移m个单位长度（0<m<3）得到另一个三角形，将所得的三角形与△ABC重叠部分的面积记为S，用m的代数式表示S．

 

Answer 1

（1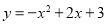）；（2）M(0，0)或M(0，－3)或M(0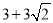，)或M(0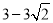，)；（3）．

【解析】

试题分析：（1）根据对称轴可知，抛物线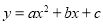与x轴的另一个交点为（﹣1，0），根据待定系数法可得抛物线的解析式为．

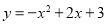（2）分三种情况：①当MA=MB时；②当AB=AM时；③当AB=BM时；三种情况讨论可得点M的坐标．

（3）平移后的三角形记为△PEF．根据待定系数法可得直线AB的解析式为y=﹣x+3．易得AB平移m个单位所得直线EF的解析式为y=﹣x+3+m．根据待定系数法可得直线AC的解析式．连结BE，直线BE交AC于G，则G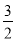（，3）．在△AOB沿x轴向右平移的过程中．根据图象，易知重叠部分面积有两种情况：①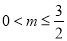当时；②当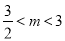时；讨论可得用m的代数式表示S．

试题解析：（1）由题意可知，抛物线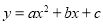与x轴的另一个交点为（﹣1，0），则：，解得：．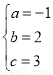

故抛物线的解析式为．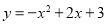

（2）依题意：设M点坐标为（0，m），

①当MA=MB时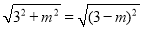：，解得m=0，故M（0，0）；

②当AB=AM时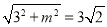：，解得m=3（舍去）或m=﹣3，故M（0，﹣3）；

③当AB=BM时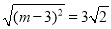，，解得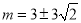，故M（0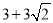，）或M（0，）．

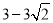所以点M的坐标为：（0，0）、（0，﹣3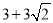）、（0，）、（0，）．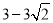

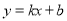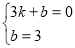（3）平移后的三角形记为△PEF．设直线AB的解析式为，则：，解得：．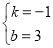

则直线AB的解析式为．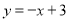

△AOB沿x轴向右平移m个单位长度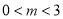（）得到△PEF，易得直线EF的解析式为．

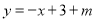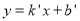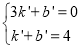设直线AC的解析式为，则：，解得：，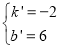

则直线AC的解析式为．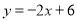

连结BE，直线BE交AC于G，则G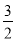（，3）．

在△AOB沿x轴向右平移的过程中．

①当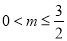时，如图1所示．

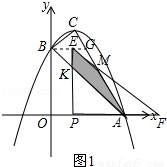
设PE交AB于K，EF交AC于M．则BE=EK=m，PK=PA=3﹣m，

联立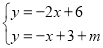，解得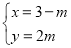：，即点M（3﹣m，2m）．

故S=S△PEF﹣S△PAK﹣S△AFM==．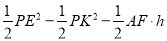

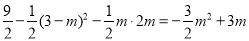②当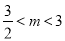时，如图2所示．

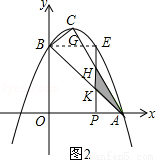
设PE交AB于K，交AC于H．因为BE=m，所以PK=PA=3﹣m，

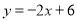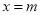又因为直线AC的解析式为，所以当时，得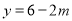，所以点H（，）．

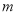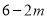故S=S△PAH﹣S△PAK=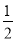PA•PH﹣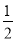PA2=．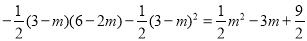

综上所述，．

考点：二次函数综合题．