
【题目】推理填空:如图,已知∠B=∠CGF,∠DGF=∠F,求证∠B+∠F=180°.
证明:∵∠B= (已知),
∴AB∥C( ),
∵∠DGF= (已知),
∴CD∥EF( ),
∴AB∥ ( )
∴∠B+ =180°( ).
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13 200元购进了一批这种衬衫,面市后果然供不应求,商家又用28 800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(1)是我们常见的“箭头图”,其中隐藏着哪些数学知识呢?下面请你解决以下问题:

(1)观察如图(1)“箭头图”,试探究∠BDC与∠A、∠B、∠C之间大小的关系,并说明理由;
(2)请你直接利用以上结论,回答下列两个问题:
①如图(2),把一块三角板XYZ放置在△ABC上,使其两条直角边XY、XZ恰好经过点B、C.若∠A=50°,则∠ABX+∠ACX= ;
②如图(3),∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4,若∠BDC=135°,∠BG1C=67°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
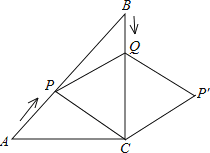
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A.![]() B.2 C.2
B.2 C.2![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0∴m=﹣3,n=3
为什么要对2n2进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程..
解决问题:
(1)若x2﹣4xy+5y2+2y+1=0,求xy的值;
(2)已知a、b、c是△ABC的三边长,满足a2+b2=10a+12b﹣61,c是△ABC中最短边的边长,且c为整数,那么c可能是哪几个数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若a是(-4)2的平方根,b的一个平方根是2,求式子a+b的立方根;
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为![]() ,求式子x2+(a+b+cd)x+
,求式子x2+(a+b+cd)x+![]() +
+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下面证明过程中的推理依据:
已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,求证∠BDE=∠C.

证明:∵AD⊥BC,FG⊥BC (已知),
∴∠ADC=∠FGC=90°____________.
∴AD∥FG______________________.
∴∠1=∠3___________________
又∵∠1=∠2,(已知),
∴∠3=∠2____________.
∴ED∥AC_____________.
∴∠BDE=∠C______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com