
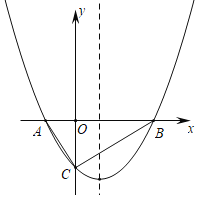
【题目】如图,已知抛物线y=![]() x2﹣
x2﹣![]() x﹣2与x轴交于A、B两点(A点在B点的左边),与y轴交于点C.点P在抛物线上,点Q在抛物线的对称轴上.若以BC为边,以点B、C、P、Q为顶点的四边形是平行四边形,求P点坐标.
x﹣2与x轴交于A、B两点(A点在B点的左边),与y轴交于点C.点P在抛物线上,点Q在抛物线的对称轴上.若以BC为边,以点B、C、P、Q为顶点的四边形是平行四边形,求P点坐标.
【答案】P点坐标为(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ).
).
【解析】
解方程![]() x2﹣
x2﹣![]() x﹣2=0得A(-1,0),B(4,0),易得C(0,-2),抛物线对称轴为直线x=
x﹣2=0得A(-1,0),B(4,0),易得C(0,-2),抛物线对称轴为直线x=![]() ,讨论:当BC为边时,四边形BCQ1P1为平行四边形,利用平移得到P1点的横坐标为
,讨论:当BC为边时,四边形BCQ1P1为平行四边形,利用平移得到P1点的横坐标为![]() ,则计算x=
,则计算x=![]() 时的二次函数值得到P点坐标;当BC为边时,四边形BCP2Q2为平行四边形,利用平移得到P2点的横坐标,则计算x=-
时的二次函数值得到P点坐标;当BC为边时,四边形BCP2Q2为平行四边形,利用平移得到P2点的横坐标,则计算x=-![]() 时对应的函数值得到此时P2点坐标;当BC为对角线时,四边形BQ3CP3为平行四边形,利用平移得到P3点的横坐标为
时对应的函数值得到此时P2点坐标;当BC为对角线时,四边形BQ3CP3为平行四边形,利用平移得到P3点的横坐标为![]() ,然后计算x=
,然后计算x=![]() 对应的函数值得到此时P3点坐标.
对应的函数值得到此时P3点坐标.
令y=0,![]() x2﹣
x2﹣![]() x﹣2=0,解得x1=﹣1,x2=4,
x﹣2=0,解得x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
当x=0时,y=![]() x2﹣
x2﹣![]() x﹣2=﹣2,则C(0,﹣2),
x﹣2=﹣2,则C(0,﹣2),
∴抛物线对称轴为直线x=![]() ,
,
当BC为边时,四边形BCQ1P1为平行四边形,C点向右平移![]() 单位得到Q1点,则B点向右平移
单位得到Q1点,则B点向右平移![]() 单位得到P1点,则P1点的横坐标为
单位得到P1点,则P1点的横坐标为![]() ,
,
当x=![]() 时,y=
时,y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() ×(
×(![]() )2﹣
)2﹣![]() ×
×![]() ﹣2=
﹣2=![]() ,
,
此时P点坐标为(![]() ,
,![]() );
);
当BC为边时,四边形BCP2Q2为平行四边形,B点向左平移![]() 单位得到Q2点,则B点向左平移
单位得到Q2点,则B点向左平移![]() 单位得到P2点,则P2点的横坐标为﹣
单位得到P2点,则P2点的横坐标为﹣![]() ,当x=﹣
,当x=﹣![]() 时,y=
时,y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() ×(﹣
×(﹣![]() )2﹣
)2﹣![]() ×(﹣
×(﹣![]() )﹣2=
)﹣2=![]() ,此时P2点坐标为(﹣
,此时P2点坐标为(﹣![]() ,
,![]() );
);
当BC为对角线时,四边形BQ3CP3为平行四边形,Q3点向左平移![]() 单位得到C点,则B点向左平移
单位得到C点,则B点向左平移![]() 单位得到P3点,则P3点的横坐标为﹣
单位得到P3点,则P3点的横坐标为﹣![]() ,当x=﹣
,当x=﹣![]() 时,y=
时,y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() ×(
×(![]() )2﹣
)2﹣![]() ×
×![]() ﹣2=
﹣2=![]() ,此时P3点坐标为(﹣
,此时P3点坐标为(﹣![]() ,
,![]() ).
).
综上所述,P点坐标为(![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某玩具商店以成本为每件60元购进一批新型玩具,以每件100元的价格销售则每天可卖出20件,为了扩大销售,增加盈利,尽快减少库存,商店决定采取适当的降价措施,经调查发现:若每件玩具每降价5元,则每天可多卖10件.
(1)若商店平均每天盈利1200元,每件玩具的售价应定为多少元?
(2)若商店为增加效益最大化,每件玩具的售价定为多少元时,商店平均每天盈利最多?最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:![]() 其中,a是方程x2+3x+1=0的根.
其中,a是方程x2+3x+1=0的根.
(2)已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(1,4)和(5,0),试求该抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.
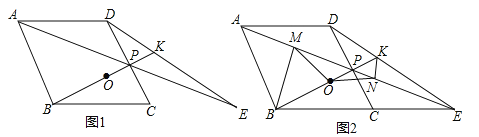
(1)求证:△ADP≌△ECP;
(2)若BP=nPK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标;
(2)已知a=1,C为抛物线与y轴的交点:
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
②在抛物线的对称轴上找出一点Q,使BQ+CQ的值最小,并求出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:
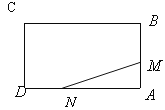
(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时间t,使![]() 的面积达到3.5cm2,若存在,求出时间t,若不存在,说明理由.
的面积达到3.5cm2,若存在,求出时间t,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
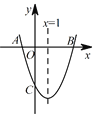
【题目】如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A,B两点,交y轴于C点,其中B点的坐标为(3,0).
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx-3的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年九龙口诗词大会在九龙口镇召开,我校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作.本次学生志愿者工作一共设置了三个岗位,分别是引导员、联络员和咨询员.
(1)若要从这5名志愿者中随机选取一位作为引导员,求选到女生的概率;
(2)若甲、乙两位志愿者都从三个岗位中随机选择一个,请你用画树状图或列表法求出他们恰好选择同一个岗位的概率.(画树状图和列表时可用字母代替岗位名称)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com