
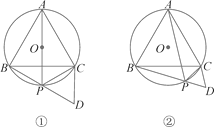
【题目】如图,等边三角形ABC的顶点在⊙O上,点P是劣弧![]() 上的一点(端点除外),延长BP至点D,使BD=AP,连结CD.
上的一点(端点除外),延长BP至点D,使BD=AP,连结CD.
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
【答案】(1)![]() 为等边三角形;(2)
为等边三角形;(2)![]() 仍为等边三角形
仍为等边三角形
【解析】
试题(1)观察图形可得△PDC为等边三角形,先根据条件证明△APC≌△BDC得出PC=DC,然后根据条件证明∠CPD=60°即可得出结论;(2)利用(1)中方法即可得出结论.
试题解析:(1)如图①,△PDC为等边三角形.(2分)
理由如下:
∵△ABC为等边三角形
∴AC=BC
∵在⊙O中,∠PAC=∠PBC
又∵AP=BD
∴△APC≌△BDC
∴PC=DC
∵AP过圆心O,AB=AC,∠BAC=60°
∴∠BAP=∠PAC=![]() ∠BAC=30°
∠BAC=30°
∴∠PBC=∠PAC=30°,∠BCP=∠BAP=30°
∴∠CPD=∠PBC+∠BCP=30°+30°=60°
∴△PDC为等边三角形;(6分)
(2)如图②,△PDC仍为等边三角形.(8分)
理由如下:
∵△ABC为等边三角形
∴AC=BC
∵在⊙O中,∠PAC=∠PBC
又∵AP=BD
∴△APC≌△BDC
∴PC=DC
∵∠BAP=∠BCP,∠PBC=∠PAC
∴∠CPD=∠PBC+∠BCP=∠PAC+∠BAP=60°
∴△PDC为等边三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 连续抛一枚均匀硬币2次有可能一次正面朝上,2次正面朝上,0次正面朝上
B. 连续抛一枚均匀硬币10次,有可能正面都朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上的次数不确定;
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的,
查看答案和解析>>
科目:初中数学 来源: 题型:
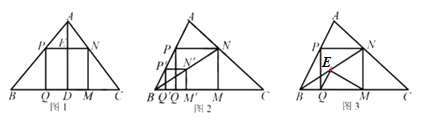
【题目】小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在△ABC中,AD⊥BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB, AC上,若BC=6,AD=4,求正方形PQMN的边长.
(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结B N′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN.小波把线段BN称为“波利亚线”.
(3)推理:证明图2中的四边形PQMN 是正方形.
(4)拓展:在(2)的条件下,于波利业线B N上截取NE=NM,连结EQ,EM(如图3).当tan∠NBM=![]() 时,猜想∠QEM的度数,并尝试证明.
时,猜想∠QEM的度数,并尝试证明.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“重整行装再出发,驰而不息再争创”,2018年5月8日兰州市召开了新一轮全国文明城市创建启动大会.某校为了更好地贯彻落实创建全国文明城市目标,举办了“我是创城小主人”的知识竞赛.该校七年级、八年级分别有300人,现从中各随机抽取10名同学的测试成绩进行调查分析,成绩如下:
七年级 | 85 | 65 | 84 | 78 | 100 | 78 | 85 | 85 | 98 | 83 |
八年级 | 96 | 60 | 87 | 78 | 87 | 87 | 89 | 100 | 83 | 96 |
整理、描述数据:
分数段 |
|
|
|
|
七年级人数 | 1 | 2 | 5 | 2 |
八年级人数 | 1 | 1 | 5 | 3 |
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七 | 84.1 | _______ | 85 |
八 | 86.3 | 87 | ______ |
得出结论:
(1)根据上述数据,将表格补充完整;
(2)估计该校七、八两个年级学生在本次测试成绩中可以取得优秀的人数![]() 共有多少人?
共有多少人?
(3)你认为哪个年级知识掌握的总体水平较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,AB=6,点D,E,F分别在边AB,BC,AC上,BD:BE=2:3,DE同时平分∠BEF和∠BDF,则BD的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校学生平均每天的体育活动时间情况,随机抽取部分学生进行问卷调查,并将调查结果人数分为A,B,C,D四个等级设活动时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.
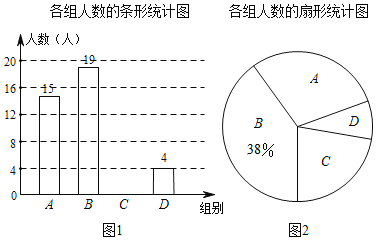
请你根据图中信息解答下列问题:
(1)该校共调查了多少名学生;
(2)将条形统计图补充完整;
(3)求出表示A等级的扇形圆心角的度数;
(4)在此次问卷调查中,甲班有2人平均每天大课间活动时间不足1小时,乙班有3人平均每天大课间活动时间不足1小时,若从这5人中任选2人去参加座谈,试用列表或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com