练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛一枚均匀硬币正面朝上的概率为，下列说法正确的是（　　）

    A. 连续抛一枚均匀硬币2次有可能一次正面朝上，2次正面朝上，0次正面朝上

    B. 连续抛一枚均匀硬币10次，有可能正面都朝上

    C. 大量反复抛一枚均匀硬币，平均每100次出现正面朝上的次数不确定；

    D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的，

    【答案】D

    【解析】

    大量反复试验时，某事件发生的频率会稳定在某个常数的附近，这个常数就叫做事件概率的估计值，而不是一种必然的结果，可得答案．

    A.连续抛一枚均匀硬币2次有可能一次正面朝上，2次正面朝上，0次正面朝上，故A错误；

    B.连续抛一枚均匀硬币10次，有可能正面都朝上，故B错误；

    C.大量反复抛一枚均匀硬币，平均每100次出现正面朝上的次数不确定，故C错误；

    D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的，故D正确；

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为发展学生的核心素养，培养学生的综合能力，某学校计划开设四门选修课：乐器、舞蹈、绘画、书法，学校采取随机抽样的方法进行问卷调查每个被调查的学生必须选择而且只能选择其中一门对调查结果进行整理，绘制成如下两幅不完整的统计图请结合图中所给信息解答下列问题：

    本次调查的学生共有______人，在扇形统计图中，m的值是______．

    分别求出参加调查的学生中选择绘画和书法的人数，并将条形统计图补充完整．

    该校共有学生2000人，估计该校约有多少人选修乐器课程？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四条直线l1：y1＝x，l2：y2＝x，l3：y3＝﹣x，l4：y4＝﹣x，OA1＝1，过点A1作A1A2⊥x轴交l1于点A2，再过点A2作A2A3⊥l1，交l2于点A3，再过点A3作A3A4⊥l2交y轴于点A4，……，则点A2020的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次数学综合实践活动中，小明计划测量城门大楼的高度，在点B处测得楼顶A的仰角为22°，他正对着城楼前进21米到达C处，再登上3米高的楼台D处，并测得此时楼顶A的仰角为45°．

    （1）求城门大楼的高度；

    （2）每逢重大节日，城门大楼管理处都要在A，B之间拉上绳子，并在绳子上挂一些彩旗，请你求出A，B之间所挂彩旗的长度（结果保留整数）．（参考数据：sin22°≈，cos22°≈，tan22°≈）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市某幼儿园六一期间举行亲子游戏，主持人请三位家长分别带自己的孩子参加游戏，主持人准备把家长和孩子重新组合完成游戏，A、B、C分别表示三位家长，他们的孩子分别对应的是a、b、c．

    （1）若主持人分别从三位家长和三位孩子中各选一人参加游戏，恰好是A、a的概率是多少（直接写出答案）

    （2）若主持人先从三位家长中任选两人为一组，再从孩子中任选两人为一组，四人共同参加游戏，恰好是两对家庭成员的概率是多少．（画出树状图或列表）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两运动员在长为100m的直道AB（A，B为直道两端点）上进行匀速往返跑训练，两人同时从A点起跑，到达B点后，立即转身跑向A点，到达A点后，又立即转身跑向B点，若甲跑步的速度为5m/s，乙跑步的速度为4m/s，则起跑后2分钟内，两人相遇的次数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论：①这个函数图象的顶点始终在直线y=-x+1上；②存在一个m的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形；③点A(x1,y1)与点B(x2,y2)在函数图象上，若x1<x2，x1+x2>2m，则y1<y2；④当-1<x<2时，y随x的增大而增大，则m的取值范围为m≥2其中错误结论的序号是（ ）

    A. ①B. ②C. ③D. ④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

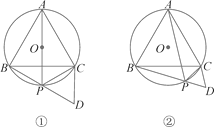
    【题目】如图，等边三角形ABC的顶点在⊙O上，点P是劣弧上的一点(端点除外)，延长BP至点D，使BD＝AP，连结CD.

    (1)若AP过圆心O，如图①，请你判断△PDC是什么三角形？并说明理由；

    (2)若AP不过圆心O，如图②，△PDC又是什么三角形？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年4月22日是第50个世界地球日，某校在八年级5个班中，每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名，学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图，请你根据图中信息解答下列问题：

    （1）求本次竞赛获奖的总人数，并补全条形统计图；

    （2）求扇形统计图中“二等奖”所对应扇形的圆心角度数；

    （3）如果该校八年级有800人，请你估计获奖的同学共有多少人？

    查看答案和解析>>

    同步练习册答案