

���� ��1�����������ߵĶԳ��ԡ������ߵĶ��������Լ��������ı߶���ȵ����ʽ��
��2���ٸ��ݴ���ϵ�����ɵ�ֱ��BD�Ľ���ʽ�����P������Ϊ��x��x2-4x+3�������H��x��x-1������G��x��3���������������i����x��1��x��4ʱ��ii����0��x��1ʱ��iii����x��0ʱ������������ۿɵõ�P�����ꣻ
�ڸ������������ε����ʿɵ�S��KPH=$\frac{3}{4}$PH2=$\frac{3}{4}$��-x2+5x-4��2���ٸ��ݶ��κ����������Կɵá�KPH��������ֵ��
��� 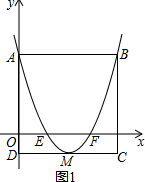 �⣺��1����ͼ1���������ߵĽ���ʽΪy=a��x-2��2-1��������M��
�⣺��1����ͼ1���������ߵĽ���ʽΪy=a��x-2��2-1��������M��
��M��2��-1����
�֡��ı���ABCD�������Σ�
��OD=1��DC=BC=AB=AD=4��
��A��0��3����
��A��0��3������y=a��x-2��2-1����
3=a��0-2��2-1��
���a=2��
�ʴ��ǣ���0��3����2��
��2������ֱ��BD�Ľ���ʽΪy=kx+b��k��0��������ֱ��BD����D��0��-1����B��4��3����
��$\left\{\begin{array}{l}{-1=b}\\{3=4k+b}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$��
��ֱ��BD�Ľ���ʽΪy=x-1��
���P��������x��x2-4x+3�������H��x��x-1������G��x��3����
i����x��1��x��4ʱ����G��PH���ӳ����ϣ���ͼ2��
��PH=2GH��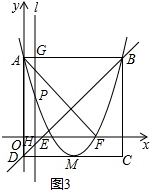
�ࣨx-1��-��x2-4x+3��=2[3-��x-1��]��
��x2-7x+12=0��
���x1=3��x2=4��
��x2=4ʱ����P��H��G�غ��ڵ�B����ȥ��
��x=3��
���ʱ��P������Ϊ��3��0����
ii����0��x��1ʱ����G��PH�ķ����ӳ����ϣ���ͼ3��PH=2GH��������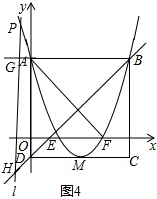
iii����x��0ʱ����G���߶�PH�ϣ���ͼ4��
��PH=2GH��
�ࣨx2-4x+3��-��x-1��=2[3-��x-1��]��
��x2-3x-4=0�����x1=-1��x2=4����ȥ����
��x=-1����ʱ��P������Ϊ��-1��8����
����������֪����P������Ϊ��3��0����-1��8����
����ͼ5����x2-4x+3=0����x1=1��x2=3��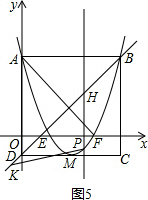 ��E��1��0����F��3��0����
��E��1��0����F��3��0����
��EF=2��
��S��AEF=$\frac{1}{2}$EF•OA=3��
�ߡ�KPH�ס�AEF��
��$\frac{{S}_{��KPH}}{{S}_{��AEF}}$=��$\frac{PH}{EF}$��2��
��S��KPH=$\frac{3}{4}$PH2=$\frac{3}{4}$��-x2+5x-4��2��
��1��x��4��
�൱x=$\frac{5}{2}$ʱ��S��KPH�����ֵΪ$\frac{243}{64}$��
���� �������˶��κ����ۺ��⣮�漰��֪ʶ���У��������ϵĵ�����������������ߵĶ���ʽ�����ε����ʣ�����ϵ������ֱ�ߵĽ���ʽ�����������ε����ʣ����κ����������ԣ�����˼�룬�ۺ��Խ�ǿ����һ�����Ѷȣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�ȱߡ�ABC����E�ڱ�AC�ϣ���D�ڱ�BC�ϣ���AE=CD������AD��BE�ཻ�ڵ�G������B��BF��AD�ڵ�F����ABG�͡�MBG����ֱ��BG�Գƣ���A�ĶԳƵ��ǵ�M����BM��AD�ཻ�ڵ�H����֪AG=3��GH=2����GE=1��
��ͼ����֪�ȱߡ�ABC����E�ڱ�AC�ϣ���D�ڱ�BC�ϣ���AE=CD������AD��BE�ཻ�ڵ�G������B��BF��AD�ڵ�F����ABG�͡�MBG����ֱ��BG�Գƣ���A�ĶԳƵ��ǵ�M����BM��AD�ཻ�ڵ�H����֪AG=3��GH=2����GE=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
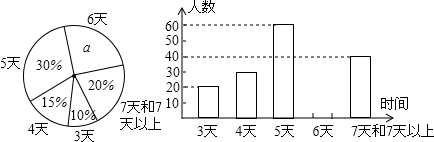
 ��ͼ����A����B����C�İ뾶����2cm����ͼ���������ε�����ĺ�Ϊ����������У�2�У�
��ͼ����A����B����C�İ뾶����2cm����ͼ���������ε�����ĺ�Ϊ����������У�2�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 17cm | B�� | 5cm | C�� | 11cm��5cm | D�� | 5cm��17cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У���C=90�㣬��AB�Ĵ�ֱƽ���߽�AB��AC�߷ֱ�Ϊ��D����E������BE��
��ͼ����ABC�У���C=90�㣬��AB�Ĵ�ֱƽ���߽�AB��AC�߷ֱ�Ϊ��D����E������BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com