
【题目】如图,四边形ABCD是平行四边形,![]() //
//![]() ,且分别交对角线AC于点E,F,连接BE,DF.
,且分别交对角线AC于点E,F,连接BE,DF.

(1)求证:AE=CF;
(2)若BE=DE,求证:四边形EBFD为菱形.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
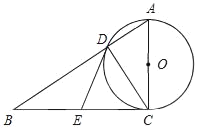
【题目】如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=6cm,DE=5cm,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
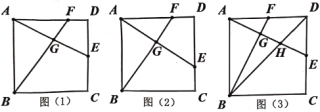
【题目】如图,正方形ABCD的边长为6,E、F分别是边CD、AD上动点,AE和BF交于点G.
(1)如图(1),若E为边CD的中点,AF=2FD,求AG的长.
(2)如图(2),若点F在AD上从A向D运动,点E在DC上从D向C运动,两点同时出发,同时到达各自终点,求在运动过程中,点G运动的路径长.
(3)如图(3),若E、F分别是边CD、AD上的中点,BD与AE交于点H,求∠FBD的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
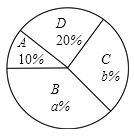
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌面上有四张正面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机翻开一张卡片,正面所标数字大于![]() 的概率为 ;
的概率为 ;
(2)随机翻开一张卡片,从余下的三张卡片中再翻开一张,求翻开的两张卡片正面所标数字之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
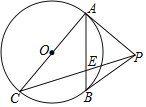
【题目】如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若∠APC=3∠BPC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,点
,点![]() ,与x轴交于另一点C,顶点为D,连接
,与x轴交于另一点C,顶点为D,连接![]() .
.
(1)求该抛物线的解析式;
(2)点P为该抛物线上一动点(与点B,C不重合),设点P的横坐标为t,
①当点P在直线![]() 的下方运动时,求
的下方运动时,求![]() 面积的最大值;
面积的最大值;
②该抛物线上是否存在点P,使得![]() ?若存在,请直接写出点P的坐标若不存在,请说明理由.
?若存在,请直接写出点P的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从机械厂购进甲、乙两种零件进行销售,若甲种零件每件的进价是乙种零件每件进价的![]() ,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
(1)求每件甲种零件和每件乙种零件的进价分别为多少元?
(2)若该商店计划购进甲、乙两种零件共110件,准备将零件批发给零售商. 甲种零件的批发价是每件100元,乙种零件的批发价是每件130元,该商店计划将这批产品全部售出从零售商处获利不低于3000元,那么该商店最多购进多少件甲种零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com