
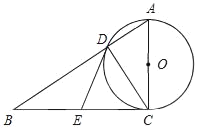
【题目】如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=6cm,DE=5cm,求⊙O直径的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
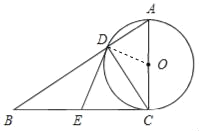
(1)连结DO,如图,根据直角三角形斜边上的中线性质,由∠BDC=90°,E为BC的中点得到DE=CE=BE,则利用等腰三角形的性质得∠EDC=∠ECD,∠ODC=∠OCD,由于∠OCD+∠DCE=∠ACB=90°,所以∠EDC+∠ODC=90°,即∠EDO=90°,于是根据切线的判定定理即可得到DE与⊙O相切;
(2)根据勾股定理和相似三角形的性质即可得到结论.
(1)证明:连结DO,如图,
∵∠BDC=90°,E为BC的中点,
∴DE=CE=BE,
∴∠EDC=∠ECD,
又∵OD=OC,
∴∠ODC=∠OCD,
而∠OCD+∠DCE=∠ACB=90°,
∴∠EDC+∠ODC=90°,即∠EDO=90°,
∴DE⊥OD,
∴DE与⊙O相切;
(2)BC=2DE=10
BD=![]() 8,
8,
∵∠BCA=∠BDC=90°,∠B=∠B,
∴△BCA∽△BDC,
![]()
![]() ∴AC=
∴AC=![]() ,
,
∴⊙O直径的长为![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
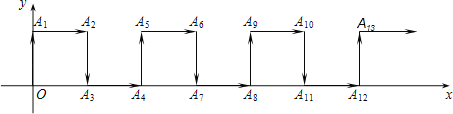
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
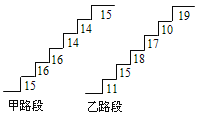
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数![]() 的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )

A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌面上有四张正面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机翻开一张卡片,正面所标数字大于![]() 的概率为 ;
的概率为 ;
(2)随机翻开一张卡片,从余下的三张卡片中再翻开一张,求翻开的两张卡片正面所标数字之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
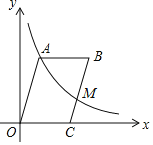
【题目】如图,OABC的周长为7,∠AOC=60°,以O为原点,OC所在直线为x轴建立直角坐标系,函数![]() (x>0)的图像经过OABC的顶点A和BC的中点M,则k的值为( )
(x>0)的图像经过OABC的顶点A和BC的中点M,则k的值为( )
A.![]() B.12C.
B.12C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,![]() //
//![]() ,且分别交对角线AC于点E,F,连接BE,DF.
,且分别交对角线AC于点E,F,连接BE,DF.

(1)求证:AE=CF;
(2)若BE=DE,求证:四边形EBFD为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com