
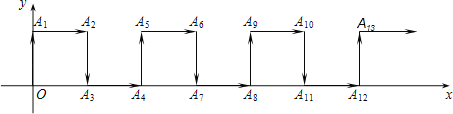
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为________________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
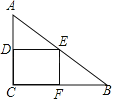
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的顶点E在边AB上,D,F两点分别在边AC,BC上,且![]() ,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
A.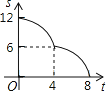 B.
B.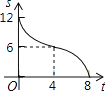 C.
C. D.
D.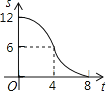
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的高,
的高, ![]() 直角
直角![]() 的顶点
的顶点![]() 是射线
是射线![]() 上一动点,
上一动点, ![]() 交直线
交直线![]() 于点
于点![]() 所在直线交直线
所在直线交直线![]() 于点F.
于点F.
(1)判断△ABC的形状,并说明理由;
(2)若G为AE的中点,求tan∠EAF的值;
(3)在点E的运动过程中,若![]() ,求
,求![]() 的值.
的值.
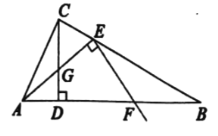
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
(Ⅰ)求点A,B和点C的坐标;
(Ⅱ)已知P是线段![]() 上的一个动点.
上的一个动点.
①若![]() 轴,交抛物线于点Q,当
轴,交抛物线于点Q,当![]() 取最大值时,求点P的坐标;
取最大值时,求点P的坐标;
②求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 在第一象限的图象交于点
在第一象限的图象交于点![]() 、点
、点![]() ,其中点
,其中点![]() 的坐标为(1,n)
的坐标为(1,n)
(1)求反比例函数解析式;
(2) 连接![]() , 求
, 求![]() 的面积;
的面积;
(3)根据图象,直接写出当![]() 时不等式
时不等式![]() 的解集
的解集
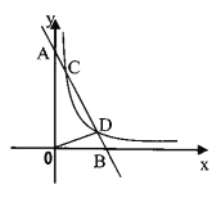
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,以AB为直径的O交BC于D,点E为AC的中点,连接DE.
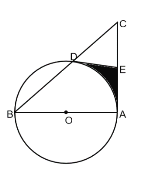
(1)求证:DE是O的切线;
(2)若∠BAD=50°,AC=6,CD=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
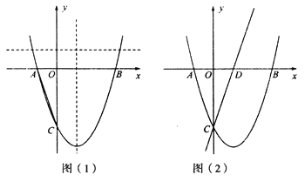
【题目】如图(1),已知抛物线![]() 与x轴交于A、B两点,与y轴负方向交于C点,且
与x轴交于A、B两点,与y轴负方向交于C点,且![]() .
.
(1)试求出抛物线的解析式;
(2)E为直线![]() 上.动点,F为抛物线对称轴上一点,当F点在对称轴上何处时,四边形ACFE的周长最短,并求出此时四边形的周长;
上.动点,F为抛物线对称轴上一点,当F点在对称轴上何处时,四边形ACFE的周长最短,并求出此时四边形的周长;
(3)如图(2),![]() 为x轴上一点,抛物线上x轴的上方是否存在点P,使得线段AP与直线CD相交且它们的夹角为45°,若存在这样的P点,请求出P点坐标;若不存在,请说明理由.
为x轴上一点,抛物线上x轴的上方是否存在点P,使得线段AP与直线CD相交且它们的夹角为45°,若存在这样的P点,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
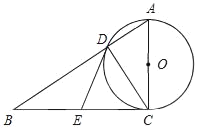
【题目】如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=6cm,DE=5cm,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
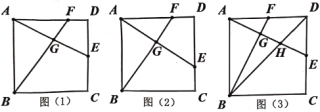
【题目】如图,正方形ABCD的边长为6,E、F分别是边CD、AD上动点,AE和BF交于点G.
(1)如图(1),若E为边CD的中点,AF=2FD,求AG的长.
(2)如图(2),若点F在AD上从A向D运动,点E在DC上从D向C运动,两点同时出发,同时到达各自终点,求在运动过程中,点G运动的路径长.
(3)如图(3),若E、F分别是边CD、AD上的中点,BD与AE交于点H,求∠FBD的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com