
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求![]() 的取值范围.
的取值范围.
(2)是否存在实数![]() ,使方程的两个实数根互为相反数?若存在,求出
,使方程的两个实数根互为相反数?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于半径为
中,对于半径为![]() 的
的![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称
,则称![]() 为
为![]() 的“近外点”.
的“近外点”.
(1)当![]() 的半径为2时,点
的半径为2时,点![]() ,
,![]() ,
,![]() ,
,![]() 中,
中,![]() 的“近外点”是__________;
的“近外点”是__________;
(2)若点![]() 是
是![]() 的“近外点”,求
的“近外点”,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)当![]() 的半径为2时,直线
的半径为2时,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若线段
,若线段![]() 上存在
上存在![]() 的“近外点”,直接写出
的“近外点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是( )
A. (-3,1) B. (3,-1) C. (-1,3) D. (1,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
已知,在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.

(1)(问题发现)
如图1,当∠EDF绕点D旋转到DE⊥AC于点E时(如图1),
①证明:△ADE≌△BDF;
②猜想:S△DEF+S△CEF= S△ABC.
(2)(类比探究)
如图2,当∠EDF绕点D旋转到DE与AC不垂直时,且点E在线段AC上,试判断S△DEF+S△CEF与S△ABC的关系,并给予证明.
(3)(拓展延伸)
如图3,当点E在线段AC的延长线上时,此时问题(2)中的结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?(写出你的猜想,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△ADE的周长为( )
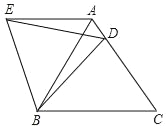
A. 19B. 20C. 27D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作矩形”的尺规作图过程,已知:![]()
求作:矩形![]()
作法:如图,
①作线段![]() 的垂直平分线角交
的垂直平分线角交![]() 于点
于点![]() ;
;
②连接![]() 并延长,在延长线上截取
并延长,在延长线上截取![]()
③连接![]()
所以四边形![]() 即为所求作的矩形
即为所求作的矩形
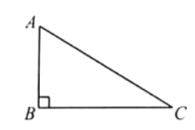
根据小东设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下边的证明:
证明:![]() ,
,![]() ,
,
![]() 四边形是平行四边形( )(填推理的依据)
四边形是平行四边形( )(填推理的依据)
![]()
![]() 四边形
四边形![]() 是矩形( )(填推理的依据)
是矩形( )(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,河南省实验中学开展了以“我和我亲爱的祖国”为主题的“快闪”活动,九年级准备从两名男生和两名女生中选出两名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为一位男生一位女生的概率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com