
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求线段AM的长.
,求线段AM的长.
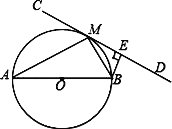
【答案】(1)证明见解析;(2)证明见解析;(3)8.
【解析】试题分析:(1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;
(2)由(1)得出的结论和直角,判断出△BME∽△BAM,即可得出结论,
(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.
试题解析:(1)如图,连接OM,
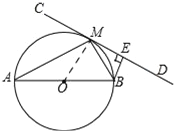
∵直线CD切⊙O于点M,
∴∠OMD=90°,
∴∠BME+∠OMB=90°,
∵AB为⊙O的直径,
∴∠AMB=90°.
∴∠AMO+∠OMB=90°,
∴∠BME=∠AMO,
∵OA=OM,
∴∠MAB=∠AMO,
∴∠BME=∠MAB;
(2)由(1)有,∠BME=∠MAB,
∵BE⊥CD,
∴∠BEM=∠AMB=90°,
∴△BME∽△BAM,
∴![]()
∴BM2=BEAB;
(3)由(1)有,∠BME=∠MAB,
∵sin∠BAM=![]() ,
,
∴sin∠BME=![]() ,
,
在Rt△BEM中,BE=![]() ,
,
∴sin∠BME=![]() =
=![]() ,
,
∴BM=6,
在Rt△ABM中,sin∠BAM=![]() ,
,
∴sin∠BAM=![]() =
=![]() ,
,
∴AB=![]() BM=10,据勾股定理得,AM=8.
BM=10,据勾股定理得,AM=8.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中正确的有( )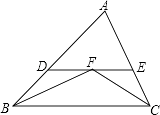
A.①②③
B.①②③④
C.①②
D.①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD.
∠BAD.
求证:EF=BE+FD;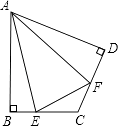
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立? 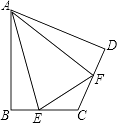
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明. 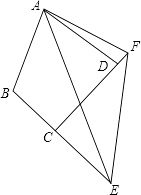
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com