
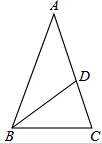
 如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,若AC=3,则BD的长为( )
如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,若AC=3,则BD的长为( )A、
| ||||
B、-3
| ||||
C、
| ||||
D、
|
| BC |
| AC |
| CD |
| BC |
| AD |
| AC |
| CD |
| AD |
| ||
| 2 |
3
| ||
| 2 |
| BC |
| AC |
| CD |
| BC |
| AD |
| AC |
| CD |
| AD |
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
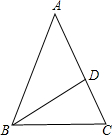
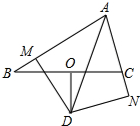 如图,△ABC中,O是BC的中点,D是∠BAC平分线上一点,且DO⊥BC,过点D分别作DM⊥AB于M,DN⊥AC于N.求证:
如图,△ABC中,O是BC的中点,D是∠BAC平分线上一点,且DO⊥BC,过点D分别作DM⊥AB于M,DN⊥AC于N.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
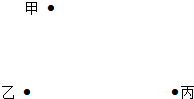 作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)
作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8,
如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8,| DO |
| BO |
| DE |
| CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
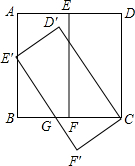 如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G
如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com