
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D. 
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
【答案】
(1)证明:连接OD,
∵OD=OB,
∴∠1=∠ODB,
∴∠DOC=∠1+∠ODB=2∠1,
而∠A=2∠1,
∴∠DOC=∠A,
∵∠A+∠C=90°,
∴∠DOC+∠C=90°,
∴OD⊥DC,
∴AC是⊙O的切线
(2)解:∵∠A=60°,
∴∠C=30°,∠DOC=60°,
在Rt△DOC中,OD=2,
∴CD= ![]() OD=2
OD=2 ![]() ,
,
∴阴影部分的面积=S△COD﹣S扇形DOE
= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]()
=2 ![]() ﹣
﹣ ![]()
【解析】(1)由OD=OB得∠1=∠ODB,则根据三角形外角性质得∠DOC=∠1+∠ODB=2∠1,而∠A=2∠1,所以∠DOC=∠A,由于∠A+∠C=90°,所以∠DOC+∠C=90°,则可根据切线的判定定理得到AC是⊙O的切线;(2)由∠A=60°得到∠C=30°,∠DOC=60°,根据含30度的直角三角形三边的关系得CD= ![]() OD=2
OD=2 ![]() ,然后利用阴影部分的面积=S△COD﹣S扇形DOE和扇形的面积公式求解.
,然后利用阴影部分的面积=S△COD﹣S扇形DOE和扇形的面积公式求解.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数![]() 的图象
的图象![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.

实验与探究:由图观察易知A(0,2)关于直线![]() 的对称点A′的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的对称点A′的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线![]() 的对称点B′、C′的位置,并写出它们的坐标: B′____________、C′___________;
的对称点B′、C′的位置,并写出它们的坐标: B′____________、C′___________;
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为____________;
的坐标为____________;
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线![]() 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:y=-![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
请结合图表完成下列各题:
(1)①表中a的值为;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是 .
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
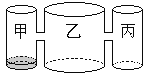
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )

A. 115° B. 105° C. 95° D. 85°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com