
【题目】如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为cm. 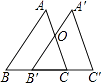
科目:初中数学 来源: 题型:
【题目】如图,三个半圆依次相外切,它们的圆心都在x轴上,并与直线y= ![]() x相切.设三个半圆的半径依次为r1、r2、r3 , 则当r1=1时,r3= .
x相切.设三个半圆的半径依次为r1、r2、r3 , 则当r1=1时,r3= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
(3)点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
(4)如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)、y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下: 参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= , b=;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE. 
(1)求证:AD∥BC;
(2)过点C作CG⊥AD于点F,交AE于点G,若AF=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的扇形纸片半径为5cm,用它围成一个圆锥的侧面,该圆锥的高是4cm,则该圆锥的底面周长是( ) 
A.3πcm
B.4πcm
C.5πcm
D.6πcm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O 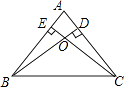
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: 
(1)甲乙两地之间的距离为千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com