
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )
),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过点C作C关于OB的对称点C′,连接AC′与OB相交,根据轴对称确定最短路线得AC′与OB的交点即为所求的点P,PA+PC的最小值=AC′,过点C′作C′D⊥OA于D,求出CC′,∠OCC′=60°,再求出CD、C′D,然后求出AD,再根据勾股定理列式计算即可得解.
解:如图,过点C作C关于OB的对称点C′,连接AC′与OB相交,
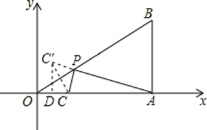
则AC′与OB的交点即所求的点P,PA+PC的最小值=AC′,
过点C′作C′D⊥OA于D,
∵点C的坐标为(1,0),且∠AOB=30°,
∴∠OCC′=90°-30°=60°,
OC=1,CC′=2×1×![]() =1,
=1,
∴CD=![]() ,C′D=
,C′D=![]() ,
,
∵顶点B的坐标为(3,![]() ),点C的坐标为(1,0),∠OAB=90°,
),点C的坐标为(1,0),∠OAB=90°,
∴AC=3-1=2,
∴AD=2+![]() =
=![]() ,
,
在Rt△AC′D中,由勾股定理得,
AC′=![]() =
=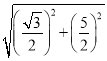 =
=![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】某服装厂里有许多剩余的三角形边角料,找出一块△ABC,测得∠C=90°(如图),现要从这块三角形上剪出一个半圆O,做成玩具,要求:使半圆O与三角形的两边AB、AC相切,切点分别为D、C,且与BC交于点E.
(1)在图中设计出符合要求的方案示意图.(要求:尺规作图,不写作法,保留作图痕迹).
(2)Rt△ABC中,AC=3,AB=5,连接AO,求出AO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点F,BH⊥AB于点B,点M是BC的中点,连接FM并延长交BH于点H.

(1)如图①所示,若∠ABC=30°,求证:DF+BH=![]() BD;
BD;
(2)如图②所示,若∠ABC=45°,如图③所示,若∠ABC=60°(点M与点D重合),猜想线段DF、BH与BD之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是
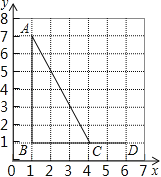
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5。一只蚂蚁如果要沿着长方体的表面从点A爬到点B,爬行的最短路程是( )
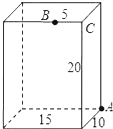
A.25B.![]() C.35D.无法确定
C.35D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,AB=8cm,BC=6cm,P、Q是
,AB=8cm,BC=6cm,P、Q是![]() 边上的两个动点,其中点P从点A开始沿A
边上的两个动点,其中点P从点A开始沿A![]() B方向运动,且速度为每秒1cm,点Q从点B开始沿B
B方向运动,且速度为每秒1cm,点Q从点B开始沿B![]() C
C![]() A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1) 出发2秒后,求PQ的长;
(2) 当点Q在边BC上运动时,通过计算说明PQ能否把![]() 的周长平分?
的周长平分?
(3) 当点Q在边AC上运动时,求能使![]() 成为等腰三角形的运动时间.
成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 | x x | |||
y | ||||
x x | x x x | |||
y y | ||||
x x x | ||||
y y | ||||
x x x | x x x x | |||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | … |
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为____,第n格的“特征多项式”为____;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一架梯子长为5m,斜靠在一面墙上,梯子底端离墙3m.如果梯子的顶端下滑了1m(如图(2)),那么梯子的底端在水平方向上滑动的距离为( ).

A.1mB.大于1m
C.不大于1mD.介于0.5m和1m之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的大小;
(2)若CD=3,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com