
在学习因式分解时,我们学习了“提公因式法”和“公式法”,事实上,除了这两种方法外,还有其它方法可以用来因式分解,比如配方法.例如,如果要因式分解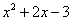 时,显然既无法用提公因式法,也无法用公式法,怎么办呢?这时,我们可以采用下面的办法:
时,显然既无法用提公因式法,也无法用公式法,怎么办呢?这时,我们可以采用下面的办法:
|
|
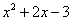 =
=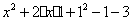

=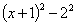
= ;
= .
解决下列问题:
(1)填空:在上述材料中,运用了 (选填一项:“分类、转化、数形结合、方程”)的思想方法,使得原题变为可以继续用平方差公式因式分解,这种方法就是配方法;
(2)显然所给材料中因式分解并未结束,请在横线上继续完成因式分解过程;
(3)请用上述方法因式分解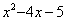 .
.
科目:初中数学 来源: 题型:
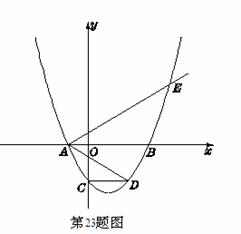
如图,二次函数y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a.
(2)求证: 为定值.
为定值.
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接GF,以线段GF,AD,AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com