
如图,二次函数y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a.
(2)求证: 为定值.
为定值.
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接GF,以线段GF,AD,AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
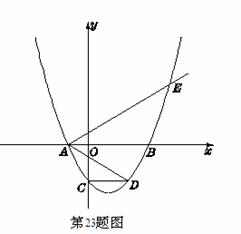
(1)解:将点C(0,-3)的坐标代入二次函数y=a(x2-2mx-3m2),
则-3=a(0-0-3m2),
解得 a=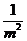 .
.
(2)证明:如图,
过点D,E分别作x轴的垂线,垂足为M,N.
由a(x2-2mx-3m2)=0,
解得 x1=-m,x2=3m,
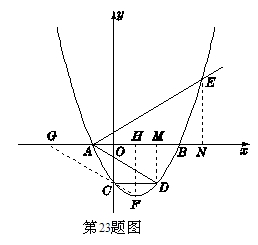 ∴ A(-m,0),B(3m,0).
∴ A(-m,0),B(3m,0).
∵ CD∥AB,
∴ 点D的坐标为(2m,-3).
∵ AB平分∠DAE,
∴∠DAM=∠EAN.
∵ ∠DMA=∠ENA=90°,
∴ △ADM∽△AEN.
∴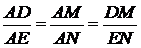 .
.
设点E的坐标为 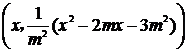 ,
,
∴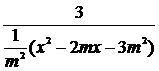 =
=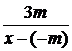 ,
,
∴ x=4m,∴ E(4m,5).
∵ AM=AO+OM=m+2m=3m,AN=AO+ON=m+4m=5m,
∴ 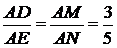 ,即为定值.
,即为定值.
(3)解:如图所示,
记二次函数图象的顶点为点F,则点F的坐标为(m,-4),
过点F作FH⊥x轴于点H.
连接FC并延长,与x轴负半轴交于一点,此点即为所求的点G.
∵ tan∠CGO=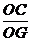 ,tan∠FGH=
,tan∠FGH=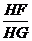 ,∴
,∴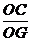 =
=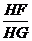 ,
,
∴ OG=3m.
此时,GF=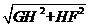 =
=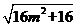 =4
=4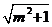 ,
,
AD=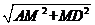 =
=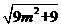 =3
=3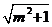 ,∴
,∴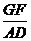 =
=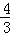 .
.
由(2)得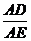 =
=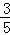 ,∴ AD︰GF︰AE=3︰4︰5,
,∴ AD︰GF︰AE=3︰4︰5,
∴ 以线段GF,AD,AE的长度为三边长的三角形是直角三角形,
此时点G的横坐标为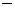 3m.
3m.


科目:初中数学 来源: 题型:
在平面直角坐标系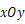 中,直线
中,直线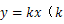 为常数)与抛物线
为常数)与抛物线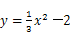 交于
交于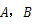 两点,且
两点,且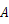 点在
点在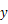 轴左侧,
轴左侧,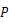 点的坐标为(0,-4),连接
点的坐标为(0,-4),连接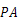 ,
,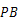 .有以下说法:
.有以下说法:
①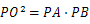 ;②当
;②当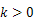 时,
时,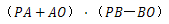 的值随
的值随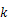 的增大而增大;
的增大而增大;
③当 -
-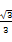 时,
时,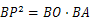 ;④△
;④△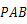 面积的最小值为4
面积的最小值为4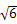 .其中正确的是 .(写出所有正确说法的序号)
.其中正确的是 .(写出所有正确说法的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
在学习因式分解时,我们学习了“提公因式法”和“公式法”,事实上,除了这两种方法外,还有其它方法可以用来因式分解,比如配方法.例如,如果要因式分解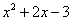 时,显然既无法用提公因式法,也无法用公式法,怎么办呢?这时,我们可以采用下面的办法:
时,显然既无法用提公因式法,也无法用公式法,怎么办呢?这时,我们可以采用下面的办法:
|
|
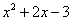 =
=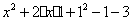

=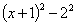
= ;
= .
解决下列问题:
(1)填空:在上述材料中,运用了 (选填一项:“分类、转化、数形结合、方程”)的思想方法,使得原题变为可以继续用平方差公式因式分解,这种方法就是配方法;
(2)显然所给材料中因式分解并未结束,请在横线上继续完成因式分解过程;
(3)请用上述方法因式分解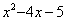 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.00 000 0076克,用科学记数法表示是
A.7.6×108克 B.7.6×10-7克 C.7.6×10-9克 D.7.6×10-8克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com