
如图,已知函数 y=3x+b 和 y=ax﹣3 的图象交于点 P(﹣2,﹣5),则根据图象可得不等式 ax﹣3
<3x+b<0 的解集是
﹣2<x<﹣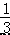 .
.
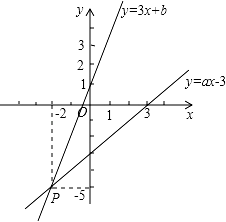
【考点】一次函数与一元一次不等式.
【分析】首先利用待定系数法把(﹣2,﹣5)代入 y=3x+b 中可得 b 的值,进而得到函数关系式,再 求出 y=3x+b 与 x 轴的交点坐标,利用图象写出不等式 ax﹣3<3x+b<0 的解集即可.
【解答】解:∵y=3x+b 经过(﹣2,﹣5),
∴﹣5=﹣6+b, 解得:b=1,
∴函数关系式为 y=3x+1, 当 y=0 时,3x+1=0,
x=﹣ 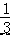 ,
,
根据图象可得 ax﹣3<3x+b<0 的解集是﹣2<x<﹣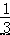 , 故答案为:﹣2<x<﹣
, 故答案为:﹣2<x<﹣  .
.
【点评】此题主要考查了一元一次不等式与一次函数的关系,关键是能从图象中得到正确信息.


科目:初中数学 来源: 题型:
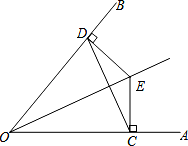
如图已知:E 是∠AOB 的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为 C、D.求证:
(1)∠ECD=∠EDC;
OE 是 CD 的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
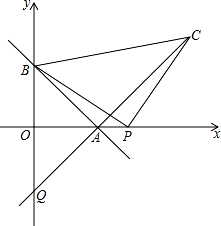
已知,如图,一次函数 y=kx+b 与 x 轴、y 轴分别交于点 A 和点 B,A 点坐标为(3,0),∠OAB=45°.
(1)求一次函数的表达式;
点 P 是 x 轴正半轴上一点,以 P 为直角顶点,BP 为腰在第一象限内作等腰 Rt△BPC,连接 CA 并延 长交 y 轴于点 Q.
①若点 P 的坐标为(4,0),求点 C 的坐标,并求出直线 AC 的函数表达式;
②当 P 点在 x 轴正半轴运动时,Q 点的位置是否发生变化?若不变,请求出它的坐标;如果变化, 请求出它的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他 惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明 a2+b2=c2.(请你写出证 明过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com