Question

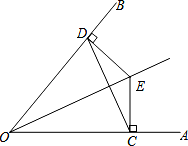
如图已知：E 是^∠AOB  的平分线上一点，EC^⊥OA，ED^⊥OB，垂足分别为 C、D．求证：

（1）^∠ECD=^∠EDC；

OE 是 CD 的垂直平分线．

Answer 1

【考点】角平分线的性质；全等三角形的判定与性质．

【专题】证明题．

【分析】（1）根据角平分线上的点到角的两边距离相等可得 EC=DE，再根据等边对等角证明即可； 利用“HL”证明 Rt^△OCE 和 Rt^△ODE 全等，根据全等三角形对应边相等可得 OC=OD，然后根据等 腰三角形三线合一证明．

【解答】证明：（1）^∵E 是^∠AOB 的平分线上一点，EC^⊥OA，ED^⊥OB，

^∴EC=DE，

^∴∠ECD=^∠EDC；

在 Rt^△OCE 和 Rt^△ODE 中，，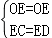

^∴Rt^△OCE≌Rt^△ODE（HL），

^∵OE 是^∠AOB 的平分线，

^∴OE 是 CD 的垂直平分线．

【点评】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，等腰 三角形三线合一的性质，熟记各性质是解题的关键．