
【题目】如图,已知函数 y=x+1 的图象与 y 轴交于点 A,一次函数 y=kx+b 的图象经过点 B(0,﹣1),与x 轴 以及 y=x+1 的图象分别交于点 C、D,且点 D 的坐标为(1,n),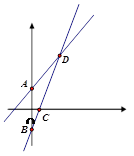
(1)则n= ,k= ,b= ;
(2)函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(3)求四边形 AOCD 的面积;
(4)在 x轴上是否存在点 P,使得以点 P,C,D 为顶点的三角形是直角三角形?若存在求出点 P 的坐标; 若不存在,请说明理由.
【答案】
(1)2,3,-1
(2)![]()
(3)解:过D作 ![]() 垂直于
垂直于 ![]() 轴,如图1所示,
轴,如图1所示,
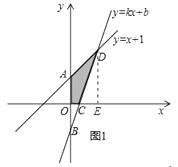
则 ![]()
![]()
![]()
(4)解:如图2, 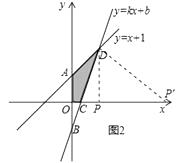
在 ![]() 轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,
轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,
理由:分两种情况考虑:
当 ![]() 时,可得
时,可得 ![]()
![]() 斜率为3,
斜率为3,
![]() 斜率为
斜率为 ![]() ,
, ![]()
![]() 解析式为
解析式为 ![]() 令
令 ![]() 即
即 ![]() 当
当 ![]() 时,由D横坐标为1,得到P点横坐标为1,
时,由D横坐标为1,得到P点横坐标为1, ![]() 在
在 ![]() 轴上,
轴上,
![]()
【解析】(1)用待定系数法求出n、k、b的值;(2)根据函数图像和D点的坐标求出X的取值范围;(3)根据图像得到S四边形AOCD=S梯形AOEDS△CDE
求出四边形 AOCD 的面积;(4)分两种情况讨论,当DP'⊥DC时,由直线DC的斜率为3,得到直线P'D斜率为![]() ,求出直线P'D解析式,由D横坐标为1,得到P点横坐标为1,得到P点的坐标.
,求出直线P'D解析式,由D横坐标为1,得到P点横坐标为1,得到P点的坐标.
【考点精析】利用确定一次函数的表达式对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】一个容量为50的样本中,数据的最大值是123,最小值是45,若取每组终点值与起点值的差为10,则该样本可以分( )
A.5组或6组
B.6组或7组
C.7组或8组
D.8组或9组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(1,3),点B(5,1).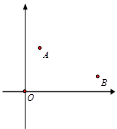
(1)只用直尺(无刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)
(2)在(1)作出点P后,点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人将一枚质量均匀的硬币连续抛10次,落地后正面朝上6次,反面朝上4次,下列说法正确的是( )
A.出现正面的频率是6
B.出现正面的频率是60%
C.出现正面的频率是4
D.出现正面的频率是40%
查看答案和解析>>
科目:初中数学 来源: 题型:
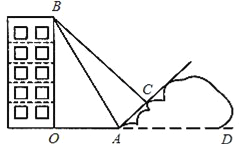
【题目】某校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动.如图,她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为60°,沿山坡往上走到C处再测得B点的仰角为45°.已知OA=200m,此山坡的坡比i=![]() ,且O、A、D在同一条直线上.
,且O、A、D在同一条直线上.
求:(1)楼房OB的高度;
(2)小红在山坡上走过的距离AC.(计算过程和结果均不取近似值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com