
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij�в�ȡ�۸�����ֶ��Դﵽ��ˮ��Ŀ�ģ��±��Ǹ�������ˮ�շѼ۸�ļ�Ŀ����
��Ŀ�� | |
ÿ����ˮ�� | ���� |
������6 m3�IJ��� | 2Ԫ/m3 |
����6 m3��������10 m3�IJ��� | 4Ԫ/m3 |
����10 m3�IJ��� | 8Ԫ/m3 |
ע��ˮ�Ѱ��½���. | |
��1����գ����û�����2�·���ˮ4 m3 �� ��Ӧ��ˮ��Ԫ��
��2�����û�����3�·���ˮa m3(����6<a<10)����Ӧ��ˮ�Ѷ���Ԫ��(�ú�a����ʽ��ʾ������)
��3�����û�����4��5�·ݹ���ˮ15 m3(5�·���ˮ��������4�·�)����4�·���ˮx m3 �� ��û�����4��5�·ݹ���ˮ�Ѷ���Ԫ��(�ú�x����ʽ��ʾ������)
���𰸡�
��1��8
��2���⣺��������ã�6![]() 2+4��a-6��=12+4a-24=4a-12��Ԫ��
2+4��a-6��=12+4a-24=4a-12��Ԫ��
��Ӧ��ˮ�ѣ�4a-12��Ԫ.
��3���⣺��5�·���ˮ��������4�·ݣ���֪��4�·���ˮ������7.5m3��
�ٵ�4�·���ˮ������5m3ʱ����5�·���ˮ������10m3��
�û�����4��5�·ݹ���ˮ��Ϊ��2x+[6![]() 2+4
2+4![]() 4+8��15-x-10��]=2x+��12+16+40-8x��=-6x+68��Ԫ����
4+8��15-x-10��]=2x+��12+16+40-8x��=-6x+68��Ԫ����
�ڵ�4�·���ˮ��������5m3����������6m3ʱ����5�·���ˮ��������9m3����������10m3��
�û�����4��5�·ݹ���ˮ��Ϊ��2x+[6![]() 2+4��15-x-6��]=2x+��12+36-4x��=-2x+48��Ԫ����
2+4��15-x-6��]=2x+��12+36-4x��=-2x+48��Ԫ����
�۵�4�·���ˮ������6m3��������7.5m3ʱ����5�·���ˮ������7.5m3������9m3��
�û�����4��5�·ݹ���ˮ��Ϊ��[6![]() 2+4��x-6��]+[6
2+4��x-6��]+[6![]() 2+4��15-x-6��]=��12+4x-24��+��12+36-4x��=36.
2+4��15-x-6��]=��12+4x-24��+��12+36-4x��=36.
�𣺸û�����4��5�·ݹ���ˮ��Ϊ��-6x+68��Ԫ��-2x+48��Ԫ��36Ԫ.
����������1����������ã�2![]() 4=8��Ԫ��
4=8��Ԫ��
�����㾫����ͨ�����������ʽ�Ӽ�����������ʽ�����㷨��1��ȥ���ţ���2���ϲ�ͬ������Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ϣ����ѧ�ƻ���������˾��A��B�����ͺŵ�С�ڰ壬��Ǣ̸������һ��A��С�ڰ�ȹ���һ��B��С�ڰ����20Ԫ���ҹ���5��A��С�ڰ����4��B��С�ڰ干��820Ԫ.
��1������һ��A��С�ڰ壬һ��B��С�ڰ����Ҫ����Ԫ��
��2������ϣ����ѧʵ����������������˾��A �� B�����ͺŵ�С�ڰ干60�飬Ҫ����A��B�����ͺŵ�С�ڰ���ܷ��ò�����5240Ԫ�����ҹ���A��С�ڰ������Ӧ���ڹ���A��B�����ͺŵ�С�ڰ��������� ![]() ������ͨ�����㣬���ϣ����ѧ��������˾��A��B�����ͺŵ�С�ڰ����ļ��ַ�����
������ͨ�����㣬���ϣ����ѧ��������˾��A��B�����ͺŵ�С�ڰ����ļ��ַ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ�½�����ԼΪ149000000km2 �� ��149000000�ÿ�ѧ��������ʾΪ�� ��
A.1.49��106
B.1.49��107
C.1.49��108
D.1.49��109
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������¶���5�棬������������3�棬����������������£���ҹ�����½���9�棬������ҹ����¶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ż������ķ�չ���������������������������ͼ�ǡ��ε�˳�糵���롰�εο쳵������ʻ���x�������Ʒ�y��Ԫ��֮��ĺ�����ϵͼ������˵����
��1�����쳵����ʻ��̲�����5����Ʒ�8Ԫ��
��2����˳�糵����ʻ��̳���2����IJ��֣�ÿ����Ʒ�1.2Ԫ��
��3��A���������6.5��10.4����
��4���ӹ�������վ����չ���ĵ������15�����˳�糵��Ҫ�ȡ��쳵������3.4Ԫ��������ȷ�ĸ����У�������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
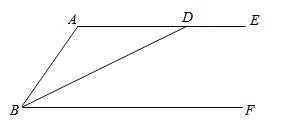
����Ŀ����ͼ����֪BDƽ�֡�ABF���ҽ�AE�ڵ�D��
��1����������BAE��ƽ����AP��Ҫ�߹���ͼ��������ͼ�ۼ�����д��������
��2����AP��BD�ڵ�O����BF�ڵ�C������CD����AC��BDʱ����֤���ı���ABCD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˶��ᾶ���У��ס���ͬʱ���ܣ����ܳ�200m���ײ���ˤ��������Ѹ�ٵ�����������Ͷ����������������ܵ�·��y��m�������ʱ��x��s���Ĺ�ϵ��ͼ��������˵���������ǽ��е���800m����������ȫ�̵�ƽ���ٶ�Ϊ6.4m/s���ۼ�ˤ��֮ǰ���ҵ��ٶȿ죻�ܼ��ٴ�Ͷ��������ƽ���ٶ�Ϊ7.5m/s���ݼ��ٴ�Ͷ��������ھ����յ�300��ʱ�����ң�������ȷ�ĸ����У�������
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��� ![]() x2����m��3��x+m2=0����������ȵ�ʵ��������ôm���������ֵ�ǣ� ��
x2����m��3��x+m2=0����������ȵ�ʵ��������ôm���������ֵ�ǣ� ��
A.2
B.1
C.0
D.��1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com