Question

【题目】在△ABC中，AB=AC，∠BAC=2∠DAE=2α．

（1）如图1，若点D关于直线AE的对称点为F，求证：△ADF∽△ABC；

（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；

（3）如图3，若α=45°，点E在BC的延长线上，则等式DE2=BD2+CE2还能成立吗？请说明理由．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）成立，理由见解析.

【解析】试题分析：（1）根据轴对称的性质可得∠EAF=∠DAE，AD=AF，再求出∠BAC=∠DAF，然后根据两边对应成比例，夹角相等两三角形相似证明；

（2）根据轴对称的性质可得EF=DE，AF=AD，再求出∠BAD=∠CAF，然后利用“边角边”证明△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠B，然后求出∠ECF=90°，最后利用勾股定理证明即可；

（3）作点D关于AE的对称点F，连接EF、CF，根据轴对称的性质可得EF=DE，AF=AD，再根据同角的余角相等求出∠BAD=∠CAF，然后利用“边角边”证明△ABD和△ACF全等，根据全等三角形对应边相等可得CF=BD，全等三角形对应角相等可得∠ACF=∠B，然后求出∠ECF=90°，最后利用勾股定理证明即可．

试题解析：（1）∵点D关于直线AE的对称点为F，

∴∠EAF=∠DAE，AD=AF，

又∵∠BAC=2∠DAE，

∴∠BAC=∠DAF，

∵AB=AC，

∴，

∴△ADF∽△ABC；

（2）∵点D关于直线AE的对称点为F，

∴EF=DE，AF=AD，

∵α=45°，

∴∠BAD=90°﹣∠CAD，

∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD，

∴∠BAD=∠CAF，

在△ABD和△ACF中，

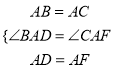
∴△ABD≌△ACF（SAS），

∴CF=BD，∠ACF=∠B，

∵AB=AC，∠BAC=2α，α=45°，

∴△ABC是等腰直角三角形，

∴∠B=∠ACB=45°，

∴∠ECF=∠ACB+∠ACF=45°+45°=90°，

在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，

所以，DE2=BD2+CE2；

（3）DE2=BD2+CE2还能成立．

理由如下：作点D关于AE的对称点F，连接EF、CF，

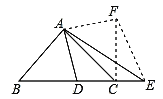
由轴对称的性质得，EF=DE，AF=AD，

∵α=45°，

∴∠BAD=90°﹣∠CAD，

∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD，

∴∠BAD=∠CAF，

由（2）得：CF=BD，∠ACF=∠B，

∵AB=AC，∠BAC=2α，α=45°，

∴△ABC是等腰直角三角形，

∴∠B=∠ACB=45°，

∴∠ECF=∠ACB+∠ACF=45°+45°=90°，

在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，

所以，DE2=BD2+CE2．