
分析 (1)因式分解法得到原方程变形为(x+9)(x-1)=0,得到两个一元一次方程,解方程即可求解;
(2)本题涉及负整数指数幂、零指数幂、特殊角的三角函数值三个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)x2+8x-9=0,
(x+9)(x-1)=0,
x+9=0,x-1=0,
解得x1=-9,x2=1.
(2)2-1+$\sqrt{2}$sin45°-20160
=$\frac{1}{2}$+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-1
=$\frac{1}{2}$+1-1
=$\frac{1}{2}$.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂等考点的运算.同时考查了解一元二次方程-因式分解法.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
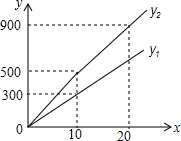 为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)×4 | B. | (-1)+(-1)+(-1)+(-1) | C. | -1×1×1×1 | D. | (-1)×(-1)×(-1)×(-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )
如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )| A. | 5 | B. | 10 | C. | 75 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com