
 如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )
如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )| A. | 5 | B. | 10 | C. | 75 | D. | 15 |
分析 分别过点A、C做AD垂直于y轴,CE垂直于x轴,根据各点坐标,既能得出各边长度,将所求三角形面积转换为直角梯形面积减去两个直接三角形的形式,套入数据,此题得解.
解答 解:过点A做AD垂直于y轴,垂直为D,则D(0,3),过点C做CE垂直于x轴,垂足为E,则E(4,0),如图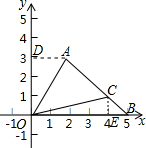
△ABC的面积=梯形DABC的面积-△ADO的面积-△OCB的面积,
由O(0,0),D(0,3),A(2,3),C(4,1),B(5,0)可知
AD=2,OD=3,OB=5,CE=1,
梯形DABC的面积=$\frac{1}{2}$×(AD+OB)×OD=$\frac{1}{2}$×(2+5)×3=$\frac{21}{2}$,
△ADO的面积=$\frac{1}{2}$×OD×AD=$\frac{1}{2}$×2×3=3,
△OCB的面积=$\frac{1}{2}$×OB×CE=$\frac{1}{2}$×5×1=$\frac{5}{2}$,
∴△ABC的面积=$\frac{21}{2}$-3-$\frac{5}{2}$=5.
故选A.
点评 本题考查坐标与图形性质以及三角形的面积,解题的关键是利用坐标与图形的性质,找到各边的长度,利用拆分法,将所要求的三角形面积转换成直角梯形面积减去两个直接三角形的形式,套入各边长度,即可求得三角形的面积.


科目:初中数学 来源: 题型:解答题
 综合与探究:
综合与探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
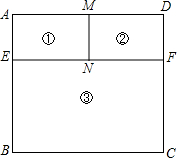 工人师傅用8米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且BE=2AE,M,N分别是AD、EF的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).
工人师傅用8米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且BE=2AE,M,N分别是AD、EF的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com