
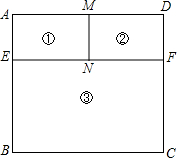
 工人师傅用8米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且BE=2AE,M,N分别是AD、EF的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).
工人师傅用8米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且BE=2AE,M,N分别是AD、EF的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).分析 (1)设AE=x米,根据已知条件表示出BC和AB的长,根据AB×BC=矩形面积2.25列出方程,解方程可得;
(2)先由长×宽=矩形面积得到函数关系式,根据公式可得函数最大值.
解答 解:(1)∵①、②、③号区域都是矩形,且BE=2AE,设AE=x米,
∴AE=MN=DF=x米,BE=CF=2x米,
∴BC=$\frac{8-7x}{3}$,
∴$\frac{8-7x}{3}$•3x=2.25,解得:x1=$\frac{1}{2}$,x2=$\frac{9}{14}$,
∴AE的长度是$\frac{1}{2}$米或$\frac{9}{14}$米;
(2)设矩形ABCD的面积是y平方米,
则y=3x•$\frac{8-7x}{3}$=-7x2+8x,
当x=-$\frac{b}{2a}$=$\frac{4}{7}$时,y最大=$\frac{4}{7}$×4=$\frac{16}{7}$,
答:当AE为$\frac{4}{7}$时,矩形窗框ABCD的透光面积最大,最大面积是$\frac{16}{7}$.
点评 本题主要考查二次函数的实际应用,表示出所需长度是解题基础,列出方程和函数关系式是关键.


科目:初中数学 来源: 题型:解答题
 已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识:
已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)×4 | B. | (-1)+(-1)+(-1)+(-1) | C. | -1×1×1×1 | D. | (-1)×(-1)×(-1)×(-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )
如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )| A. | 5 | B. | 10 | C. | 75 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,下列说法正确的是( )
如图所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,下列说法正确的是( )| A. | ∠2+∠3>∠1 | B. | ∠2+∠3<∠1 | C. | ∠2+∠3=∠1 | D. | 无法判断 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com