
 已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识:
已知,建立如图所示的直角坐标系,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识:分析 (1)用长方形的面积减去三个小三角形的面积即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
(3)设直线AC的函数表达式为y=kx+b,把A(0,3),C(8,4)代入得出方程组,解方程组即可.
解答 解:(1)△ABC的面积=4×8-1×8÷2-2×3÷2-6×4÷2=13.
故△ABC的面积为13;
(2)△ABC是直角三角形;理由如下:
∵正方形小方格边长为1
∴AC=$\sqrt{{1}^{2}+{8}^{2}}$=$\sqrt{65}$,AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,BC=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,
∵在△ABC中,AB2+BC2=13+52=65,AC2=65,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
(3)设直线AC的函数表达式为y=kx+b,
把A(0,3),C(8,4)代入得:$\left\{\begin{array}{l}{b=3}\\{8k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{8}}\\{b=3}\end{array}\right.$,
∴直线AC的函数表达式为y=$\frac{1}{8}$x+3.
点评 本题考查了正方形的性质,三角形的面积,勾股定理,勾股定理的逆定理,用待定系数法求直线的解析式;熟练掌握勾股定理、勾股定理的逆定理以及待定系数法是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC.
如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 综合与探究:
综合与探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
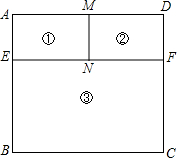 工人师傅用8米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且BE=2AE,M,N分别是AD、EF的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).
工人师傅用8米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且BE=2AE,M,N分别是AD、EF的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com