
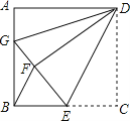
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:
①△DAG≌△DFG:②BG=2AG;③S△DGF=120;④S△BEF=![]() ,其中所有正确结论有:______.
,其中所有正确结论有:______.
【答案】①②④
【解析】
①根据直角三角形的HL全等判定方法,即得![]() 与
与![]() 全等;
全等;
②先设![]() ,进而将
,进而将![]() 三边用含
三边用含![]() 的式子表示,再根据勾股定理列出方程求解即得;③根据折叠的性质及正方形的性质得出
的式子表示,再根据勾股定理列出方程求解即得;③根据折叠的性质及正方形的性质得出![]() ,再根据全等的性质得出
,再根据全等的性质得出![]() ,最后即可算出
,最后即可算出![]() ;
;
④先计算出![]() ,再根据
,再根据![]() 即得
即得![]() .
.
解:如图,由折叠可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
在Rt△ADG和Rt△FDG中,
![]() ,
,
∴Rt△ADG≌Rt△FDG(HL),故①正确;
∵正方形边长是12,
∴BE=EC=EF=6,
设AG=FG=x,则EG=x+6,BG=12-x,
由勾股定理得:EG2=BE2+BG2,
即:(x+6)2=62+(12-x)2,
解得:x=4
∴AG=GF=4,BG=8,BG=2AG,故②正确;
∵GF=4,DF=AB=12
∴![]() 故③错误;
故③错误;
∵BG=8,BE=6
∴![]()
∵![]() ,EG=EF+GF=10
,EG=EF+GF=10
∴S△BEF=![]() S△GBE=
S△GBE=![]() ×24=
×24=![]() ,故④正确.
,故④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于点D,DE⊥AB于E.若△ADE的周长为8cm,则AB=_____ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是![]()
![]()
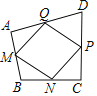
A. 当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B. 当M,N,P,Q是各边中点,且![]() 时,四边形MNPQ为正方形
时,四边形MNPQ为正方形
C. 当M,N、P,Q是各边中点,且![]() 时,四边形MNPQ为菱形
时,四边形MNPQ为菱形
D. 当M,N、P、Q是各边中点,且![]() 时,四边形MNPQ为矩形
时,四边形MNPQ为矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
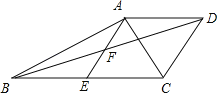
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,
(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-![]() .
.
(1)将y=-![]() +x+
+x+![]() 用配方法化为y=a(x-h)2+k的形式;
用配方法化为y=a(x-h)2+k的形式;
(2)求该函数图象与两坐标轴交点的坐标;
(3)画出该函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数![]() (k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO=
(k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO=![]() ,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,
,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,
(1)求该反比例函数和一次函数的解析式;
(2)连接ED,求△ADE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com