
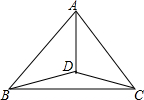
 如图,AB=AC,∠CBD=∠BCD,∠BDC=150°,求∠BDA的度数.
如图,AB=AC,∠CBD=∠BCD,∠BDC=150°,求∠BDA的度数. 分析 根据∠CBD=∠BCD,得到BD=CD,证明△ABD≌△ACD,得到∠ADB=∠ADC,再根据∠ADB+∠ACD+∠BDC=360°,∠BDC=150°,即可解答.
解答 解:∵∠CBD=∠BCD,
∴BD=CD,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD,
∴∠ADB=∠ADC,
∵∠ADB+∠ACD+∠BDC=360°,∠BDC=150°,
∴∠ADB+∠ACD=110°,
∴∠BDA=110°÷2=55°.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△ABD≌△ACD.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日 期 | 7 | 8 | 9 | 10 | 11 | 12 |
| 水位记录 | +1.41 | +0.09 | -0.04 | +0.09 | -0.45 | -0.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
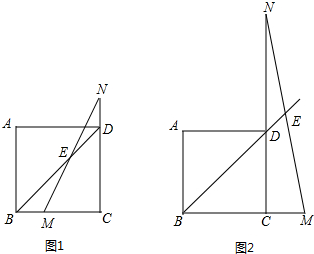
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
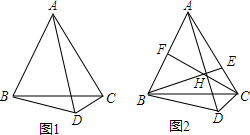
查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).
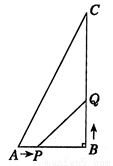
(1)当 时,求△PBQ的面积;
时,求△PBQ的面积;
(2)当 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当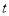 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com