
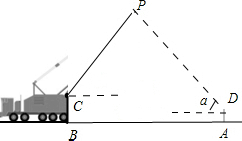
 如图,是一辆吊车的示意图,小明站在距吊车底部点B为10米的A处看到吊车的起重臂顶端P处的仰角a为45°,已知吊车的起重臂底端C处与地面的距离(线段BC的长)为3.2米,起重臂CP与水平方向的夹角β为53.1°,小明的眼睛D处距地面为1.6米,求吊车的起重臂CP的长度和点P到地面的距离.(参考数据:sin53.1°≈0.8,cos53.1°≈0.6,tan53.1°≈$\frac{3}{4}$)
如图,是一辆吊车的示意图,小明站在距吊车底部点B为10米的A处看到吊车的起重臂顶端P处的仰角a为45°,已知吊车的起重臂底端C处与地面的距离(线段BC的长)为3.2米,起重臂CP与水平方向的夹角β为53.1°,小明的眼睛D处距地面为1.6米,求吊车的起重臂CP的长度和点P到地面的距离.(参考数据:sin53.1°≈0.8,cos53.1°≈0.6,tan53.1°≈$\frac{3}{4}$) 分析 过点P作PE⊥AB于E,分别过点C和点D作CM⊥PE于M,作DN⊥PE于点N,在Rt△PCM中,得到CM=$\frac{PM}{tanβ}$=$\frac{x}{tan53.1°}$=$\frac{3}{4}$x,在Rt△PND中,得到ND=$\frac{PN}{tanα}$=$\frac{x+1.6}{tan45°}$=x+1.6,然后根据PE=PM+ME,求出PE的长.
解答 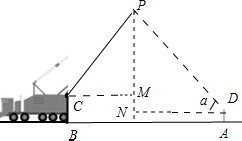 解:过点P作PE⊥AB于E,分别过点C和点D作CM⊥PE于M,作DN⊥PE于点N,如图所示,
解:过点P作PE⊥AB于E,分别过点C和点D作CM⊥PE于M,作DN⊥PE于点N,如图所示,
则ME=BC=3.2m,EN=AD=1.6m,
因此MN=ME-EN=3.2-1.6=1.6(m)
设PM=x米,则PN=PM+MN=x+1.6(米)
在Rt△PCM中,CM=$\frac{PM}{tanβ}$=$\frac{x}{tan53.1°}$=$\frac{3}{4}$x.
在Rt△PND中,ND=$\frac{PN}{tanα}$=$\frac{x+1.6}{tan45°}$=x+1.6.
因为CM+ND=BE+EA=BA=10(米),所以$\frac{3}{4}$x+x+1.6=10,
解得,x=4.8.
因此PM=4.8米.
所以,在Rt△PCM中,PC=$\frac{PM}{sinβ}$=$\frac{4.8}{0.8}$=6米.
PE=PM+ME=4.8+3.2=8(米),
答:吊车的起重臂CP的长度为6米,点P到地面的距离为8米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,找到相关三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
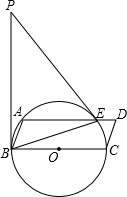 如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.
如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
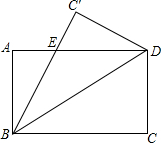 如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )| A. | ∠ABE=∠C′DE | B. | EB=ED | C. | EA=EC′ | D. | ∠ABE等于30° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
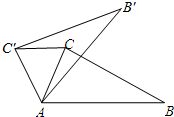 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB等于50°.
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得C′C∥AB,则∠B′AB等于50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.49×102人 | B. | 7.49×104人 | C. | 7.49×106人 | D. | 0.749×107人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com