
【题目】定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在![]() 与
与![]() 中,
中,![]() ,且
,且![]() 所以称
所以称![]() 与
与![]() 为“关联等腰三角形”,设它们的顶角为
为“关联等腰三角形”,设它们的顶角为![]() ,连接
,连接![]() ,则称
,则称![]() 会为“关联比".
会为“关联比".
下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
![]() 当
当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,
时,
①在图1中,若点![]() 落在
落在![]() 上,则“关联比”
上,则“关联比”![]() =
=
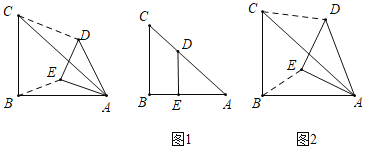
②在图2中,探究![]() 与
与![]() 的关系,并求出“关联比”
的关系,并求出“关联比”![]() 的值.
的值.

[类比探究]
![]() 如图3,
如图3,
①当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() =
=
②猜想:当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() = (直接写出结果,用含
= (直接写出结果,用含![]() 的式子表示)
的式子表示)
[迁移运用]
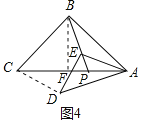
![]() 如图4,
如图4, ![]() 与
与![]() 为“关联等腰三角形”.若
为“关联等腰三角形”.若![]() 点
点![]() 为
为![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 为
为![]() 上一动点,求点
上一动点,求点![]() 自点
自点![]() 运动至点
运动至点![]() 时,点
时,点![]() 所经过的路径长.
所经过的路径长.
【答案】(1)①![]() ;②
;②![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]()
【解析】
(1)①由α=90°可得△ABC与△AED为等腰直角三角形,斜边AC=![]() AB,AD=
AB,AD=![]() AE,而DC=AC-AD,EB=AB-AE,代入计算即求得
AE,而DC=AC-AD,EB=AB-AE,代入计算即求得![]() =
=![]() .
.
②由△ABC与△AED为等腰直角三角形可得∠BAC=∠EAD=45°,减去公共角∠CAE得∠CAD=∠BAE,再加上两夹边成比例,证得△CAD∽△BAE,所以![]() 等于相似比
等于相似比![]() .
.
(2)①过点E作EF⊥AD于点F,由α=120°可得∠EAD=30°,所以得到Rt△AED的三边比,则AE=2EF,AF=![]() EF,进而有AD=2AF=2
EF,进而有AD=2AF=2![]() EF,代入计算即求得
EF,代入计算即求得![]() =
=![]() .
.
②由α=n°可得∠EAD=90°-![]() ,又因为cos∠EAD=
,又因为cos∠EAD=![]() ,所以得AF=AEcos(90°-
,所以得AF=AEcos(90°-![]() ),AD=2AF=2AEcos(90°-
),AD=2AF=2AEcos(90°-![]() ),根据①的证明过程可得
),根据①的证明过程可得![]() =
=![]() =2cos(90°-
=2cos(90°-![]() ).
).
(3)过点B作BF⊥AC于点F,根据等腰直角三角形的条件求得PB的长,即求得点E自点B运动至点P时BE的长.连接CD,由(1)②的证明过程可知△CAD∽△BAE,所以∠ACD=∠ABE为一个定角,即点D所经过的路径是线段CD.根据“关联比”![]() 的值为
的值为![]() ,求得CD=
,求得CD=![]() EB=
EB=![]() ×
×![]() =
=![]() .
.
解:(1)①∵当![]() 时,
时,![]() 与
与![]() 为等腰直角三角形
为等腰直角三角形 ![]()
![]()
![]()
故答案为: ![]()
②当![]() 时,
时,
![]() 均为等腰直角三角形
均为等腰直角三角形
![]()
![]()
![]()
又![]()
![]()
![]()
![]() “关联比”
“关联比”![]() 为
为![]()
![]() ①过点E作EF⊥AD于点F
①过点E作EF⊥AD于点F
∴∠AFE=90°
∵AE=DE,∠AED=α=120°
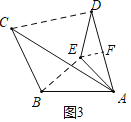
∴∠EAD=∠EDA=30°,AF=DF
∴AE=2EF,AF=![]() EF
EF
∴AD=2AF=2![]() EF
EF
∴![]()
同理可证:∠BAC=30°,![]()
∴∠EAD+∠CAE=∠BAC+∠CAE
即∠CAD=∠BAE
∴△CAD∽△BAE
![]()
故答案为:![]() .
.
②过点E作EF⊥AD于点F
![]()
![]()
![]()
![]() 中,
中,![]()
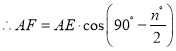
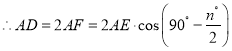
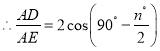
由①的证明过程可得 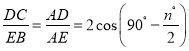
故答案为:2cos 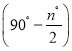
![]() 如图,过点
如图,过点![]() 作
作![]() 于点
于点![]()
∵![]() 与
与![]() 为“关联等腰三角形",
为“关联等腰三角形",
![]() ,
,
![]() 与
与![]() 均为等腰直角三角形,
均为等腰直角三角形,![]()
∵![]()
![]()
连接![]() ,由上可知.
,由上可知.![]() ≌
≌![]()
![]() =定角,
=定角,
![]() 点
点![]() 所经过的路径是线段
所经过的路径是线段![]()
∵![]() 时,“关联比”为
时,“关联比”为![]() ,
,
![]() 当点
当点![]() 自点
自点![]() 运动至点
运动至点![]() 时,
时,
点![]() 所经过的路径
所经过的路径![]()


科目:初中数学 来源: 题型:
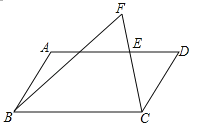
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
科目:初中数学 来源: 题型:
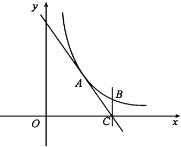
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(1)求k的值与B点的坐标;
(2)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,试写出符合条件的所有D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
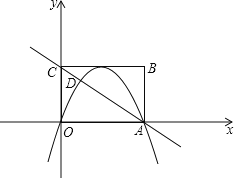
(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】樱桃是我市的特色时令水果.一上市,水果店的老板用2400元购进一批樱桃,很快售完;老板又用3700元购进第二批樱桃,进价比第一批每千克少了11元,所购件数是第一批2的倍.
(1)第一批樱桃进价是每千克多少元?
(2)老板以每千克50元的价格销售第二批樱桃,售出80%后,为了尽快售完,剩下降价促销、要使得第二批樱桃的销售利润不低于1100元,剩余的樱桃每千克最多降价多少元销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
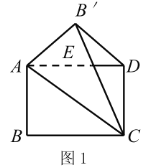
【题目】实践操作
如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 落在矩形
落在矩形![]() 所在平面内,
所在平面内,![]() 和
和![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
解决问题
(1)在图1中,①![]() 和
和![]() 的位置关系为__________;②将
的位置关系为__________;②将![]() 剪下后展开,得到的图形是_____;
剪下后展开,得到的图形是_____;
(2)若图1中的矩形变为平行四边形时![]() ,如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;
,如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由;
拓展应用
(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形,则小红折叠的矩形纸片的长宽之比为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com