
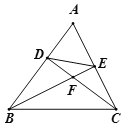
【题目】如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点F.
(1)求证: ![]() ;
;
(2)请探究线段DE,CE的数量关系,并说明理由;
(3)若CD⊥AB,AD=2,BD=3,求线段EF的长.
【答案】(1)证明见解析;(2)DE=CE,理由见解析;(3)![]() .
.
【解析】试题分析:(1)证明△ABE∽△ACD,从而得出结论;
(2) 先证明∠CDE=∠ACD,从而得出结论;
(3)解直角三角形示得.
试题解析:
(1)∵∠ABE=∠ACD,∠A=∠A,
∴△ABE∽△ACD,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
又∵∠A=∠A,
∴△ADE∽△ACB,
∴∠AED=∠ABC,
∵∠AED=∠ACD+∠CDE,∠ABC=∠ABE+∠CBE,
∴∠ACD+∠CDE=∠ABE+∠CBE,
∵∠ABE=∠ACD,
∴∠CDE=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠CDE=∠ABE=∠ACD,
∴DE=CE;
(3)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠CDE+∠ADE=90°,
∵∠ABE=∠ACD,∠CDE=∠ACD,
∴∠A=∠ADE,∠BEC=∠ABE+∠A=∠A+∠ACD=90°,
∴AE=DE,BE⊥AC,
∵DE=CE,
∴AE=DE=CE,
∴AB=BC,
∵AD=2,BD=3,
∴BC=AB=AD+BD=5,
在Rt△BDC中, ![]() ,
,
在Rt△ADC中, ![]() ,
,
∴![]() ,
,
∵∠ADC=∠FEC=90°,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
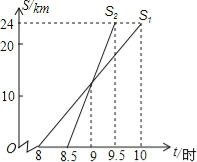
A. 小亮骑自行车的平均速度是12km/h
B. 妈妈比小亮提前0.5小时到达姥姥家
C. 妈妈在距家12km处追上小亮
D. 9:30妈妈追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市旅游景区有A,B,C,D,E等著名景点,该市旅游部门统计绘制出2018年春节期间旅游情况统计图(如图),根据图中信息解答下列问题:
(1)2018年春节期间,该市A,B,C,D,E这五个景点共接待游客 万人,扇形统计图中E景点所对应的圆心角的度数是 ,并补全条形统计图.
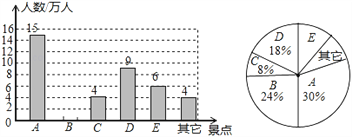
(2)甲,乙两个旅行团在A,B,D三个景点中随机选择一个,这两个旅行团选中同一景点的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
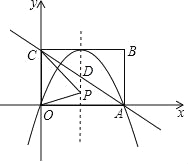
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交AC于点D,动点P在抛物线对称轴上,动点Q在抛物线上.
(1)求抛物线的解析式;
(2)当PO+PC的值最小时,求点P的坐标;
(3)是否存在以A,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级数学教师邱龙从家里出发,驾车去离家![]() 的风景区度假,出发一小时内按原计划的速度匀速行驶,一小时后以原速的1.5倍匀速行驶,并提前40分钟到达风景区;第二天返回时以去时原计划速度的1.2倍行驶回到家里.那么来回行驶时间相差_________分钟.
的风景区度假,出发一小时内按原计划的速度匀速行驶,一小时后以原速的1.5倍匀速行驶,并提前40分钟到达风景区;第二天返回时以去时原计划速度的1.2倍行驶回到家里.那么来回行驶时间相差_________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读,并完成填空与证明:
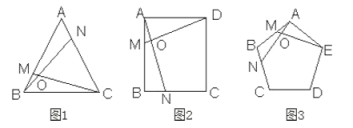
初二(8)、(9)班数学兴趣小组展示了他们小组探究发现的结果,内容为:图1,正三角形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,发现利用“
,发现利用“![]() ”证明
”证明![]() ≌
≌![]() ,可得到
,可得到![]() ,
,![]() ,再利用三角形的外角定理,可求得
,再利用三角形的外角定理,可求得![]()
(1)图2正方形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,那么
,那么![]() ,且
,且![]() 度,请证明你的结论.
度,请证明你的结论.
(2)图3正五边形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,那么
,那么![]() ,且
,且![]() 度;
度;
(3)请你大胆猜测在正![]() 边形中的结论:
边形中的结论:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司举行周年庆典,决定订购一批印有公司logo的记事本赠送给客户,购买甲种记事本共花费3000元,购买乙种记事本共花费2100元,购买甲种记事本的数量是购买乙种记事本数量的2倍,且购买一个乙种记事本比购买一个甲种记事本多花20元.
(1)求购买一个甲种记事本,一个乙种记事本各需多少元?
(2)由于公司业务的扩大,公司决定再次购买甲、乙两种记事本共40个,且乙种记事本不少于23个,预算金额不超过2400元,购买时恰逢该店对两种记事本的售价进行调整,甲种记事本售价比第一次购买时提高了10%,乙种记事本售价比第一次购买时降低了10%,请问该公司有哪几种方案购买这批记事本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com