
【题目】八年级数学教师邱龙从家里出发,驾车去离家![]() 的风景区度假,出发一小时内按原计划的速度匀速行驶,一小时后以原速的1.5倍匀速行驶,并提前40分钟到达风景区;第二天返回时以去时原计划速度的1.2倍行驶回到家里.那么来回行驶时间相差_________分钟.
的风景区度假,出发一小时内按原计划的速度匀速行驶,一小时后以原速的1.5倍匀速行驶,并提前40分钟到达风景区;第二天返回时以去时原计划速度的1.2倍行驶回到家里.那么来回行驶时间相差_________分钟.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
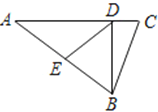
【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC.
(2)若E是边AB上的动点,求线段DE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
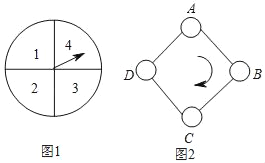
【题目】如图1,是一个材质均匀可自由转动的转盘,转盘的四个扇形面积相等,分别有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每转动转盘一次,当转盘停止运动时,指针所落扇形中的数字是几(当指针落在四个扇形的交线上时,重新转动转盘),就沿正方形的边顺时针方向连续跳几个边长.
如:若从图A起跳,第一次指针所落扇形中的数字是3,就顺时针连线跳3个边长,落到圈D;若第二次指针所落扇形中的数字是2,就从D开始顺时针续跳2个边长,落到圈B;……设游戏者从圈A起跳.
(1)嘉嘉随机转一次转盘,求落回到圈A的概率P1;
(2)琪琪随机转两次转盘,用列表法求最后落回到圈A的概率P2,并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
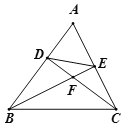
【题目】如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点F.
(1)求证: ![]() ;
;
(2)请探究线段DE,CE的数量关系,并说明理由;
(3)若CD⊥AB,AD=2,BD=3,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,点
中,点![]() 是边
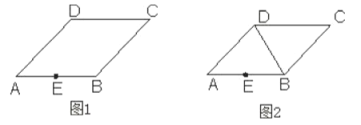
是边![]() 的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
(1)在图1中,过点![]() 画
画![]() 的平行线;
的平行线;
(2)在图2中,连接![]() ,在
,在![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() 的距离之和最短.
的距离之和最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
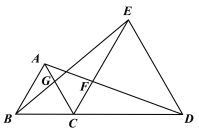
【题目】如图,点C为线段BD上一点,△ABC、△CDE都是等边三角形.AD与CE交于点F,BE与AC相交于点G.
(1)求证:△ACD≌△BCE;
(2)若CF+CG=8,BD=18,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:![]() >0.
>0.
解:设![]() =0,解得:
=0,解得:![]() =0,
=0,![]() =5,则抛物线y=
=5,则抛物线y=![]() 与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=
与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=![]() 的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即![]() >0,所以,一元二次不等式
>0,所以,一元二次不等式![]() >0的解集为:x<0或x>5.
>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式![]() <0的解集为 .
<0的解集为 .
(3)用类似的方法解一元二次不等式:![]() >0.
>0.
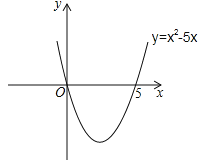
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com