
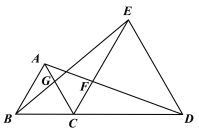
【题目】如图,点C为线段BD上一点,△ABC、△CDE都是等边三角形.AD与CE交于点F,BE与AC相交于点G.
(1)求证:△ACD≌△BCE;
(2)若CF+CG=8,BD=18,求△ACD的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明∠BCE=∠DCA,再利用全等三角形判定定理(SAS)证明△ACD≌△BCE;
(2)过G,F作BD垂线段,分别交BD的垂线段GM,FN,证明△BCG≌△ACF,得出CG=CF=4,得出GM和FN的值,再代入面积公式求出△ACD的面积
(1)∵△ABC,△CDE是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°
∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠DCA
∴△ACD≌△BCE
(2)由(1)得△ACD≌△BCE,∴∠CBG=∠CAF
又∵∠ACF=∠BCG=60°,BC=AC,∴△BCG≌△ACF
∴![]() ,CG=CF,而CF+CG=8,∴CG=CF=4
,CG=CF,而CF+CG=8,∴CG=CF=4
过G,F作BD垂线段,分别交BD的垂线段GM,FN
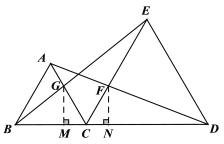
又∵∠ACB=∠DCE=60°
∴GM=![]() CG=2
CG=2![]()
FN=![]() CF=2
CF=2![]()
∴![]()
=![]()
=![]()
=![]()
=![]()
=![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级数学教师邱龙从家里出发,驾车去离家![]() 的风景区度假,出发一小时内按原计划的速度匀速行驶,一小时后以原速的1.5倍匀速行驶,并提前40分钟到达风景区;第二天返回时以去时原计划速度的1.2倍行驶回到家里.那么来回行驶时间相差_________分钟.
的风景区度假,出发一小时内按原计划的速度匀速行驶,一小时后以原速的1.5倍匀速行驶,并提前40分钟到达风景区;第二天返回时以去时原计划速度的1.2倍行驶回到家里.那么来回行驶时间相差_________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
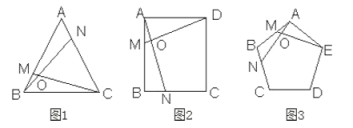
【题目】请阅读,并完成填空与证明:
初二(8)、(9)班数学兴趣小组展示了他们小组探究发现的结果,内容为:图1,正三角形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,发现利用“
,发现利用“![]() ”证明
”证明![]() ≌
≌![]() ,可得到
,可得到![]() ,
,![]() ,再利用三角形的外角定理,可求得
,再利用三角形的外角定理,可求得![]()
(1)图2正方形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,那么
,那么![]() ,且
,且![]() 度,请证明你的结论.
度,请证明你的结论.
(2)图3正五边形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,那么
,那么![]() ,且
,且![]() 度;
度;
(3)请你大胆猜测在正![]() 边形中的结论:
边形中的结论:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在一个不透明的口袋中装有3个红球和一个白球,它们除了颜色外其他都相同。
(1)若从这个口袋中随机地取出1个球,则“取出的球恰好是白球”的概率是_______;
(2)若从这个口袋中随机地一次性取出2个球,再问问先用树状图或者列表的方法得到所有的结果,然后再求“取出的2个球恰好都是红球”的概率是多少?
(3)若往这个口袋中又加入了与袋中红球一样的若干个红球,在搅匀袋子之后,进行下面随机试验:随机地抽取1个球,记录它的颜色后又放回口袋中,......,我们如此很多次重复做这个试验后发现,取出红球的频率一直稳定在95%附近,那么请你求一下大约又加入了多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你认为其中正确信息的个数有
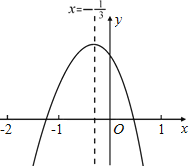
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司举行周年庆典,决定订购一批印有公司logo的记事本赠送给客户,购买甲种记事本共花费3000元,购买乙种记事本共花费2100元,购买甲种记事本的数量是购买乙种记事本数量的2倍,且购买一个乙种记事本比购买一个甲种记事本多花20元.
(1)求购买一个甲种记事本,一个乙种记事本各需多少元?
(2)由于公司业务的扩大,公司决定再次购买甲、乙两种记事本共40个,且乙种记事本不少于23个,预算金额不超过2400元,购买时恰逢该店对两种记事本的售价进行调整,甲种记事本售价比第一次购买时提高了10%,乙种记事本售价比第一次购买时降低了10%,请问该公司有哪几种方案购买这批记事本?
查看答案和解析>>
科目:初中数学 来源: 题型:
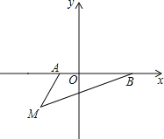
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+2|+(b﹣4)2=0.
(1)填空:a=_____,b=_____;
(2)如果在第三象限内有一点M(﹣3,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=﹣3时,在y轴上有一点P,使得△ABP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com