
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交AC于点D,动点P在抛物线对称轴上,动点Q在抛物线上.
(1)求抛物线的解析式;
(2)当PO+PC的值最小时,求点P的坐标;
(3)是否存在以A,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.
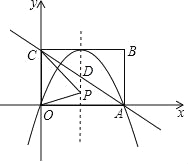
【答案】(1)y=![]() x2+3x;(2)当PO+PC的值最小时,点P的坐标为(2,
x2+3x;(2)当PO+PC的值最小时,点P的坐标为(2,![]() );(3)存在,具体见解析.
);(3)存在,具体见解析.
【解析】
试题(1)由条件可求得抛物线的顶点坐标及A点坐标,利用待定系数法可求得抛物线解析式;
(2) 连接PA,D与P重合时有最不值,求出点D的坐标即可;
(3)存在,分别以PA,PC、PC,PQ、PA,PQ为一组邻边时,写出坐标即可;
试题解析:
(1)在矩形OABC中,OA=4,OC=3,
∴A(4,0),C(0,3),
∵抛物线经过O、A两点,且顶点在BC边上,
∴抛物线顶点坐标为(2,3),
∴可设抛物线解析式为y=a(x﹣2)2+3,
把A点坐标代入可得0=a(4﹣2)2+3,解得a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣2)2+3,即y=
(x﹣2)2+3,即y=![]() x2+3x;
x2+3x;
(2)连接PA,
∵点P在抛物线对称轴上,∴PA=PO,∴PO+PC= PA+PC.
当点P与点D重合时,PA+PC= AC;
当点P不与点D重合时,PA+PC> AC;
∴当点P与点D重合时,PO+PC的值最小,
设直线AC的解析式为y=kx+b,
根据题意,得![]() 解得
解得
∴直线AC的解析式为![]() ,
,
当x=2时,![]() ,
,
∴当PO+PC的值最小时,点P的坐标为(2,![]() );
);
(3)存在.当以PA,PC为一组邻边时,P(2,0),Q(2,3);
当以PC,PQ为一组邻边时,P(2,-6),Q(6,-9);
当以PA,PQ为一组邻边时,P(2,-12),Q(-2,-9).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,这批书包进人市场后发现供不应求,商店又购进第二批同样的书包,且所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司快递员甲匀速骑车前往某小区送物件,出发几分钟后,快递员乙发现甲的手机落在公司,无法联系,于是乙匀速骑车去追赶甲.乙刚出发2分钟时,甲也发现自己手机落在公司,立刻按原路原速骑车回公司,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回公司,甲继续原路原速赶往某小区送物件,甲乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(乙给甲手机的时间忽略不计).则乙回到公司时,甲距公司的路程是______米.
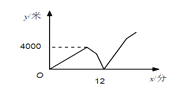
查看答案和解析>>
科目:初中数学 来源: 题型:
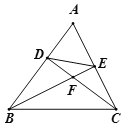
【题目】如图,在△ABC中,点D,E分别在边AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于点F.
(1)求证: ![]() ;
;
(2)请探究线段DE,CE的数量关系,并说明理由;
(3)若CD⊥AB,AD=2,BD=3,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=![]() .若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨梅是漳州的特色时令水果,杨梅一上市,某水果店的老板用1 200元购进一批杨梅,很快售完;该老板又用2 500元购进第二批杨梅,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批杨梅每件进价是多少元?
(2)老板以每件150元的价格销售第二批杨梅,售出80%后,为了尽快售完,决定打折促销,要使第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折?(利润=售价-进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com