
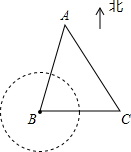
 ��ɳȺ���Թ����������й�������������ɳȺ����ֻӴ���ֵ������й��Ŀ��ƣ���Ͻ���������֮һ���Գ�Ͻ�ΪԲ�ģ�����Χ12���ﷶΧ�ھ����ڽ�����������������ֻ���룮����һ�й����ബ������A������14����/Сʱ���ٶ���λ�ڳ�Ͻ�������B����ƫ��15��ĺ�����Ѳ�ߣ����ബ�ϵ�ֵ����Ա�����ڳ�Ͻ�����������24������һ������洬������C����������10����/Сʱ���ٶ�����������ʻ���Ͻ����з�����������洬�������棬��ʱ����洬���й����ബ����ƫ��30��ķ����ϣ���ͼ��ʾ��
��ɳȺ���Թ����������й�������������ɳȺ����ֻӴ���ֵ������й��Ŀ��ƣ���Ͻ���������֮һ���Գ�Ͻ�ΪԲ�ģ�����Χ12���ﷶΧ�ھ����ڽ�����������������ֻ���룮����һ�й����ബ������A������14����/Сʱ���ٶ���λ�ڳ�Ͻ�������B����ƫ��15��ĺ�����Ѳ�ߣ����ബ�ϵ�ֵ����Ա�����ڳ�Ͻ�����������24������һ������洬������C����������10����/Сʱ���ٶ�����������ʻ���Ͻ����з�����������洬�������棬��ʱ����洬���й����ബ����ƫ��30��ķ����ϣ���ͼ��ʾ������ ��1������C����B������CD���е�ΪD������BD������ֱ�������ε����ʵõ���BCD=30�㣬�õ��𰸣�
��2������B��BE��AC���������ҵĸ������BE���������ҵĸ������AB��
��3�������������AC�ij��������ٶȡ����롢ʱ��Ĺ�ϵ��ʽ���㼴�ɣ�
��� �⣺��1������C����B������CD���е�ΪD������BD��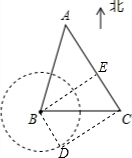
��BD��CD��
������ɵ�BC=24��BD=12��
����Rt��BCD�У���BCD=30�㣬
�����ת���ر�ƫ��60�㺽�У�����ǡ�ñ�������Ͻ�12���������
��2������B��BE��AC����AC�ڵ�E��
������ã���ACB=60�㣮
��BE��AC��
���CBE=30�㣬sin��ACB=$\frac{BE}{BC}$=$\frac{\sqrt{3}}{2}$��
�֡�BC=24��
��BE=12$\sqrt{3}$��
�֡�ABC=75�㣬
���ABE=45�㣬
��AB=12$\sqrt{6}$��
���й����ബ���Ͻ�֮��ľ���Ϊ12$\sqrt{6}$���
��3����CE=12��AE=12$\sqrt{3}$��
��AC=12+12$\sqrt{3}$��32.76�������
���й����ബ���ٶ�Ϊ14����/Сʱ������洬���ٶ�Ϊ10����/Сʱ��������������̾��������У�
��32.76�£�14+10��=1.365��Сʱ����
�����洬�ϵIJ��˾���1.365Сʱ����Եõ�������
���� ���⿼����ǽ�ֱ�������ε�Ӧ��-��������⣬��ȷ��ע����ǡ����������Ǻ����ĸ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 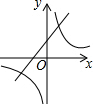 | B�� | 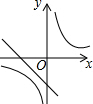 | C�� | 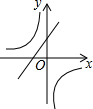 | D�� | 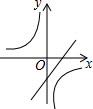 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
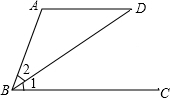 ��ͼ����֪AD��BC����A����ABC=2��1����1=��2�����ADB�Ķ�����
��ͼ����֪AD��BC����A����ABC=2��1����1=��2�����ADB�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3$+2\sqrt{2}$ | B�� | 3$-\sqrt{2}$ | C�� | 17$+12\sqrt{2}$ | D�� | 17-12$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
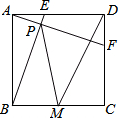 ��ͼ��������ABCD�У�AB=4������E�ӵ�A�������D�˶���ͬʱ����F�ӵ�D�������C�˶�����E��F�˶����ٶ���ͬ�������ǵ�������յ�ʱֹͣ�˶����˶��������߶�AF��BE�ཻ�ڵ�P��M���߶�BC������һ�㣬��MD+MP����СֵΪ2$\sqrt{10}$��
��ͼ��������ABCD�У�AB=4������E�ӵ�A�������D�˶���ͬʱ����F�ӵ�D�������C�˶�����E��F�˶����ٶ���ͬ�������ǵ�������յ�ʱֹͣ�˶����˶��������߶�AF��BE�ཻ�ڵ�P��M���߶�BC������һ�㣬��MD+MP����СֵΪ2$\sqrt{10}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com