

分析 (1)根据抛物线过原点,顶点为(2,-2)即可确定抛物线解析式;
(2)先确定点A关于BC的对称点A′,求出直线AA′的解析式,进一步求出与BC的交点即为点P的坐标;
(3)先确定直线AQ的解析式,再联立抛物线求出点Q坐标,分析即可确定三角形形状.
解答 解:(1)根据题意知
$\left\{\begin{array}{l}{0=c}\\{-\frac{b}{2a}=2}\\{-2=4a+2b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-2}\\{c=0}\end{array}\right.$.
故抛物线的解析式为y=$\frac{1}{2}$x2-2x.
(2)作点A关于直线BC的对称点A′,连接PA′,如图1所示.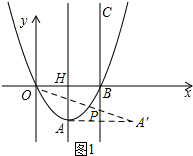
由对称的特性可知,PA=PA′,
当O、P、A′三点共线时,PO+PA′=OA′最小.
令y=$\frac{1}{2}$x2-2x=0,解得:x1=0,x2=4,
∴B点坐标为(4,0),直线BC解析式:x=4.
∵A、A′关于直线BC对称,且A点坐标为(2,-2),
∴A′点坐标为(6,-2).
又∵O点坐标为(0,0),
∴直线OA′的解析式为y=-$\frac{1}{3}$x.
∴当O、P、A′三点共线时有$\left\{\begin{array}{l}{y=-\frac{1}{3}x}\\{x=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=4}\\{y=-\frac{4}{3}}\end{array}\right.$.
故当PO+PA的值最小时,点P的坐标为(4,-$\frac{4}{3}$).
(3)如图2,
当射线AH′经过点P时,求得射线AO'与 x轴交点K的坐标为(3,0),
设直线AK:y=mx+n,
把点A(2,-2),K(3,0)代入得:
$\left\{\begin{array}{l}{-2=2m+n}\\{0=3m+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=2}\\{n=-6}\end{array}\right.$,
∴直线AK:y=2x-6,
联立:$\left\{\begin{array}{l}{y=2x-6}\\{y=\frac{1}{2}{x}^{2}-2x}\end{array}\right.$,
解得:x=6,或x=2(舍去)
此时y=6,
所以点Q(6,6),
直线AK交 抛物线于点Q,其坐标为(6,6),
可求∠QOB=45°,∠BOA=45°,
易证∠QOA=90°,所以△QOA为直角三角形;
当射线AO'经过点P时,△QOA为钝角三角形.
点评 此题主要考查二次函数的综合问题,会求抛物线解析式以及与直线的交点,会求对称点解决线段和最短问题;会运用旋转解决相关问题,判断三角形形状是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 9 | D. | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
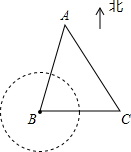 南沙群岛自古以来就是中国的领土,但南沙群岛中只哟部分岛屿受中国的控制,赤瓜礁就是其中之一.以赤瓜礁为圆心,在周围12海里范围内均属于禁区,不允许他国船只进入.今有一中国海监船(记作A)正以14海里/小时的速度在位于赤瓜礁(记作B)北偏东15°的海域中巡逻,海监船上的值班人员发现在赤瓜礁的正东方向24海里有一艘外国渔船(记作C),其正以10海里/小时的速度沿正西方向驶向赤瓜礁,中方立即向外国渔船发出警告,此时外国渔船在中国海监船的南偏东30°的方向上,如图所示.
南沙群岛自古以来就是中国的领土,但南沙群岛中只哟部分岛屿受中国的控制,赤瓜礁就是其中之一.以赤瓜礁为圆心,在周围12海里范围内均属于禁区,不允许他国船只进入.今有一中国海监船(记作A)正以14海里/小时的速度在位于赤瓜礁(记作B)北偏东15°的海域中巡逻,海监船上的值班人员发现在赤瓜礁的正东方向24海里有一艘外国渔船(记作C),其正以10海里/小时的速度沿正西方向驶向赤瓜礁,中方立即向外国渔船发出警告,此时外国渔船在中国海监船的南偏东30°的方向上,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com