
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
(1)求抛物线的解析式;
(2)若直线AM′与此抛物线的另一个交点为C,求△CAB的面积;
(3)是否存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.
【答案】
(1)解:将A、B点坐标代入函数解析式,得 ![]() ,
,
解得 ![]() ,
,
抛物线的解析式y=x2﹣2x﹣3
(2)解:将抛物线的解析式化为顶点式,得
y=(x﹣1)2﹣4,
M点的坐标为(1,﹣4),
M′点的坐标为(1,4),
设AM′的解析式为y=kx+b,
将A、M′点的坐标代入,得
![]() ,
,
解得 ![]() ,
,
AM′的解析式为y=2x+2,
联立AM′与抛物线,得
![]() ,
,
解得 ![]() ,
, ![]()
C点坐标为(5,12).
S△ABC= ![]() ×4×12=24
×4×12=24
(3)解:存在过A,B两点的抛物线,其顶点P关于x轴的对称点为Q,使得四边形APBQ为正方形,
由ABPQ是正方形,A(﹣1,0)B(3,0),得
P(1,﹣2),Q(1,2),或P(1,2),Q(1,﹣2),
①当顶点P(1,﹣2)时,设抛物线的解析式为y=a(x﹣1)2﹣2,
将A点坐标代入函数解析式,得
a(﹣1﹣1)2﹣2=0,
解得a= ![]() ,
,
抛物线的解析式为y= ![]() (x﹣1)2﹣2,
(x﹣1)2﹣2,
②当P(1,2)时,设抛物线的解析式为y=a(x﹣1)2+2,将
A点坐标代入函数解析式,得
a(﹣1﹣1)2+2=0,
解得a=﹣ ![]() ,
,
抛物线的解析式为y=﹣ ![]() (x﹣1)2+2,
(x﹣1)2+2,
综上所述:y= ![]() (x﹣1)2﹣2或y=﹣
(x﹣1)2﹣2或y=﹣ ![]() (x﹣1)2+2,使得四边形APBQ为正方形.
(x﹣1)2+2,使得四边形APBQ为正方形.
【解析】(1)根据待定系数法,将A、B点坐标代入函数解析式,即可求解。
(2)先求出顶点坐标,根据轴对称的性质,可求得点M′的坐标,再求出直线AM′的解析式,再将两函数解析式联立,建立方程组,求解即可求出点C的坐标,然后求出△ABC的面积。
(3)根据正方形的性质,求得P、Q两点的坐标,根据待定系数法,可得函数解析式。
【考点精析】掌握确定一次函数的表达式和正方形的性质是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.不论a为何值,函数图象必经过(2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现】:如图1,在正三角形ABC中,在AB,AC边上分别取点M,N,BM=AN,连接BN,CM,相交于点O,求∠α
易得:△ABN≌△BCN,则∠1=∠2
∵∠α是△BOC的外角,∴∠α=∠2+∠3
∴∠α=∠1+∠3=∠ABC=60°
【推广】:在正n边形中,对相邻的两边实施同样的操作…
(1)如图2,在正四边形ABCD中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(2)如图3,在正五边形ABCDE中,在AB,AD边上分别取点M,N,连接BN,CM,可确定∠α=°;
(3)判断:∠α可以等于160°吗?如果可以,求出对应的边数n,若不可以,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
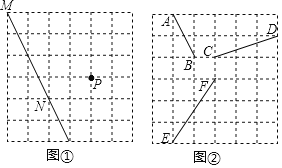
【题目】如图,在6×6的正方形网格中,每个小正方形的边长为1,点A、B、C、D、E、F、M、N、P均为格点(格点是指每个小正方形的顶点).
(1)利用图①中的网格,过P点画直线MN的平行线和垂线.
(2)把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形).
(3)第(2)小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店3月份经营一种热销商品,每件成本20元,发现三周内售价在持续提升,销售单价P(元/件)与时间t(天)之间的函数关系为P=30+ ![]() t(其中1≤t≤21,t为整数),且其日销售量y(件)与时间t(天)的关系如下表
t(其中1≤t≤21,t为整数),且其日销售量y(件)与时间t(天)的关系如下表
时间t(天) | 1 | 5 | 9 | 13 | 17 | 21 |
日销售量y(件) | 118 | 110 | 102 | 94 | 86 | 78 |
(1)已知y与t之间的变化规律符合一次函数关系,请直接写出y(件)与时间t(天)函数关系式;
(2)在这三周的销售中,第几天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的21天中,该网店每销售一件商品就捐赠a元利润(a<8)给“精准扶贫”的对象,通过销售记录发现,这21天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.

(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
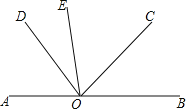
【题目】如图,已知,A、O、B在同一条直线上,∠AOE=∠COD,∠EOD=30°.
(1)若∠AOE=88°30′,求∠BOC的度数;
(2)若射线OC平分∠EOB,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )
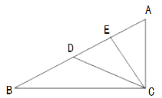
A. 5cm B. 6cm C. 7cm D. 8cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com