【题目】如图，在数轴上，点
表示1，现将点沿
轴做如下移动，第一次点向左移动3个单位长度到达点
，第二次将点向右移动6个单位长度到达点
，第三次将点向左移动9个单位长度到达点
，按照这种移动规律移动下去，第
次移动到点
，如果点与原点的距离不小于20，那么的最小值是__________．
【答案】13
【解析】
序号为奇数的点在点A的左边，各点所表示的数依次减少3，序号为偶数的点在点A的右侧，各点所表示的数依次增加3，于是可得到A13表示的数为-17-3=-20，A12表示的数为16+3=19，则可判断点An与原点的距离不小于20时，n的最小值是13．
解：第一次点A向左移动3个单位长度至点A1，则A1表示的数，1-3=-2；
第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为-2+6=4；
第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4-9=-5；
第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为-5+12=7；
第5次从点A4向左移动15个单位长度至点A5，则A5表示的数为7-15=-8；
…；
则A7表示的数为-8-3=-11，A9表示的数为-11-3=-14，A11表示的数为-14-3=-17，A13表示的数为-17-3=-20，
A6表示的数为7+3=10，A8表示的数为10+3=13，A10表示的数为13+3=16，A12表示的数为16+3=19，
所以点An与原点的距离不小于20，那么n的最小值是13．
故答案为：13．
科目：初中数学 来源： 题型：
【题目】如图,在平面直角坐标系中有一点A(4,-1),将点A向左平移5个单位再向上平移5个单位得到点B,直线
过点A、B,交x轴于点C,交y轴于点D, P是直线上的一个动点,通过研究发现直线上所有点的横坐标x与纵坐标y 都是二元一次方程x+y=3的解.
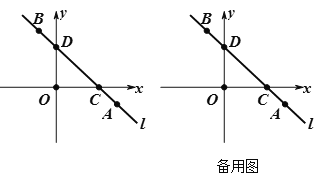
①直接写出点B,C,D的坐标；B_______, C_________, D________
②求
③当
时,求点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知:二次函数y=-x2+bx+c的图象过点(-1,-8),(0,-3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x-h)2+k的形式;
(2)用五点法画出此函数图象的示意图.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆货车从超市出发，向东行驶了
千米到达小彬家，继续向东行驶了
千米到达小颖家，然后向西行驶了
千米到达小明家，最后回到超市．
（1）以超市为原点，向东为正，以
个单位长度表示
，在数轴上表示出上述各地点的位置．
（2）请列式计算小明家在超市什么方向？距超市多远？
（3）若货车每千米油耗
升，这辆货车共耗油多少升？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】陈老师为了解七班
同学对新闻、体育、娱乐、动画四类电视节目的喜欢情况，调查了全班
名同学(每名同学必选且只能选择这四类节目中的一类)，并将调查结果绘制成如下不完整的条形统计图和扇形统计图．根据两图提供的信息，解答下列问题:
求喜欢娱乐节目的人数，并将条形统计图补充完整；
求扇形统计图中喜欢体育节目的人数占全班人数的百分比和圆心角
的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零.由此可得：如果mx+n=0，其中m、n为有理数，x为无理数，那么m=0且n=0.
（1）如果
，其中a、b为有理数，那么a= ，b= .
（2）如果
，其中a、b为有理数，求a+2b的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）
（2）（-36.35）+（-7.25）+26.35+（+7
）
（3）（﹣99）﹣（+61）﹣（﹣52）+（﹣32）
（4） 49
+(－78.21)+27
+(－21.79)
（5）
（6）
（7）
（8）
（9） 
（10）
(11) 
（12）
（13）
(计算不简便不得分)
（14）| —1+（—2
）| +（—1
）
（15）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
