
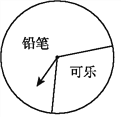
【题目】某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(如图所示).下表是活动进行中的一组统计数据:
转动转盘 的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
落在“铅笔” 区域的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔” 区域的频率 |
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得哪种奖品的机会大?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?
【答案】(1)0.68,0.74,0.68,0.69,0.705,0.701;(2)0.7;(3)铅笔;(4)252°.
【解析】分析:(1)根据频率的算法:频率=频数总数可得各个频率,据此填空即可;
(2)、(3)根据频率的定义,可得当n很大时,频率将会接近其概率进行解答;
(4)根据扇形图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比计算即可.
本题解析:
解:(1)如下表所示:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
落在“铅笔”区域的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”区域的频率 | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
(2)当n很大时,落在“铅笔”区域的频率将会接近0.7.
(3)获得铅笔的机会大.
(4)扇形的圆心角约是0.7×360°=252°.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°. 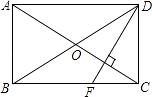
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于0.25,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )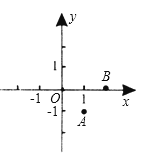
A.(3,-1)
B.(-1,-1)
C.(1,1)
D.(-2,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com