
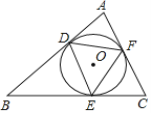
【题目】如图,![]() 的内切圆
的内切圆![]() 与各边分别相切于点
与各边分别相切于点![]() ,
,![]() ,
,![]() ,那么下列叙述错误的是( )
,那么下列叙述错误的是( )
A. 点![]() 是
是![]() 的三条角平分线的交点 B. 点
的三条角平分线的交点 B. 点![]() 是
是![]() 的三条中线的交点
的三条中线的交点
C. 点![]() 是
是![]() 的三条边的垂直平分线的交点 D.
的三条边的垂直平分线的交点 D. ![]() 一定是锐角三角形
一定是锐角三角形
【答案】B
【解析】
根据切线的性质得到OD⊥AB,OE⊥BC,OF⊥AC,根据同圆的半径相等得到OD=OE=OF,于是得到点O是△ABC的三条角平分线的交点,根据外接圆的圆心的性质得到点O是△DEF的三条边的垂直平分线的交点,根据四边形的内角和和圆周角定理得到DEF是锐角三角形.
连接OD,OE,OF,

∵△ABC的内切圆O与各边分别相切于点D,E,F,
∴OD⊥AB,OE⊥BC,OF⊥AC,
∵OD=OE=OF,
∴点O是△ABC的三条角平分线的交点,
∵⊙O是△DEF的外接圆,
∴点O是△DEF的三条边的垂直平分线的交点,
∵∠ADO=∠AFO=90°,
∴∠A+∠DOF=180°,
∴∠DOF=180°-∠A,
∴∠DEF=![]() ∠DOF=90°-
∠DOF=90°-![]() ∠A,
∠A,
∴∠DEF是锐角,同理∠EDF与∠DFE是锐角,
∴△DEF是锐角三角形,
故选B.


科目:初中数学 来源: 题型:
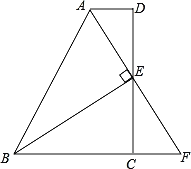
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
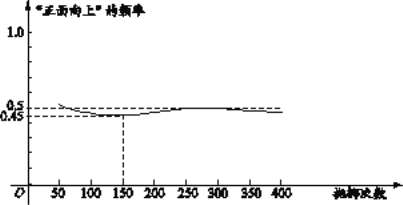
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进![]() 、
、![]() 两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中
两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中![]() 种苗的单价为8元/棵,购买
种苗的单价为8元/棵,购买![]() 种苗所需费用
种苗所需费用![]() (元)与购买数量
(元)与购买数量![]() (棵)之间存在如图所示的函数关系.
(棵)之间存在如图所示的函数关系.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若在购买计划中,![]() 种苗的数量不超过35棵,但不少于
种苗的数量不超过35棵,但不少于![]() 种苗数量的一半,请设计购买方案,使总费用最低,并求出最低费用.
种苗数量的一半,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
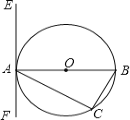
【题目】已知:如图,三角形![]() 内接于
内接于![]() ,
,![]() 为直径,过点
为直径,过点![]() 作直线
作直线![]() ,要使得
,要使得![]() 是
是![]() 的切线,还需添加的条件是(只需写出三种):①________或②________或③________.
的切线,还需添加的条件是(只需写出三种):①________或②________或③________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为
为![]() 的中点,点
的中点,点![]() 、
、![]() 、
、![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 上的一点,
上的一点,![]() 以
以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,![]() ,连结
,连结![]() .
.
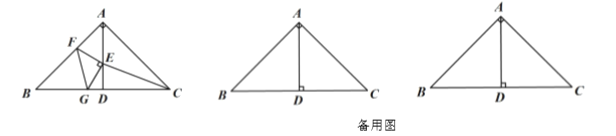
(1)当![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长.
的长.
(2)当![]() 时,求
时,求![]() 的面积.
的面积.
(3)①比较![]() 与
与![]() 的面积大小关系,并说明理由.
的面积大小关系,并说明理由.
②当![]() 的面积为6时,求
的面积为6时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
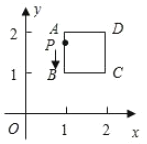
【题目】如图,平面直角坐标系中,在边长为1的正方形![]() 的边上有—动点
的边上有—动点![]() 沿正方形运动一周,
沿正方形运动一周,![]() 则
则![]() 的纵坐标
的纵坐标![]() 与点
与点![]() 走过的路程
走过的路程![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
A. 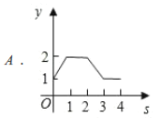 B.
B. 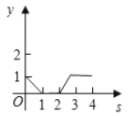 C.
C. 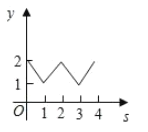 D.
D. 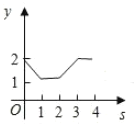
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com