
【题目】在ABCD中,AB=5,BC=10,BC边上的高AM=4,过BC边上的动点E(不与点B,C重合)作直线AB的垂线,EF与DC的延长线相交于点G.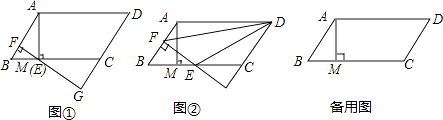
(1)如图①,当点E与点M重合时,求EF的长;
(2)如图②,当点E为BC的中点时,连结DE,DF,求△DEF的面积;
(3)当点E在BC上运动时,△BEF与△CEG的周长之间有何关系?请说明理由.
【答案】
(1)
解:如图①,
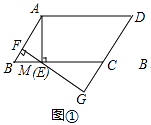
∵AB=5,AM=4,AM⊥BC,
∴BM= ![]() =
= ![]() =3,
=3,
∵S△ABM= ![]() AMBM=
AMBM= ![]() ABEF,
ABEF,
∴EF= ![]() =
= ![]() =
= ![]() .
.
(2)
解:如图②,
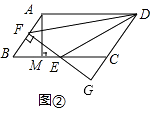
∵E为BC中点,BC=10,
∴BE=CE=5,
∴AB=BE=5,
∵EF⊥AB,AM⊥BC,
∴∠AMB=∠EFB=90°,
∵∠B=∠B,
∴△ABM≌△EBF,
∴EF=AM=4,BF=BM=3,
∵四边形ABCD为平行四边形,
∴AB∥DG,
∴FG⊥DG,∠B=∠ECG,
∵∠BFE=∠G=90°,
∴△BEF≌△CEG,
∴CG=BF=3,EF=EG=4,
∴DG=CD+CG=5+3=8,
∴S△DEF= ![]() EFDG=
EFDG= ![]() ×4×8=16;
×4×8=16;
(3)
解:图③,
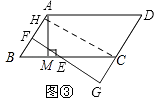
过点C作CH⊥AB,垂足为H,
∴HC⊥DG,
∴四边形HFGC为矩形,
∴HC=FG=8,CG=FH,
∴BH= ![]() =
= ![]() =6,
=6,
∵△BFE和△CEG的周长之和为:BE+EF+BF+EC+CG+EG,
=BC+FG+BH,
=10+8+6,
=24,
∴△BEE与△CEG的周长之和为定值24.
【解析】(1)先由勾股定理求BM的长,再利用面积法求EF;(2)要想求△DEF的面积,需要求底边EF和高DG的长,先证明△ABM≌△EBF,得EF=AM=4,再证明FG⊥DG,证明△BEF≌△CEG,得CG=3,求出DG=8,代入面积公式可以求△DEF的面积;(3)过点C作CH⊥AB,垂足为H,利用勾股定理求BH的长,写出△BEF与△CEG的周长之和,发现:EF+EG=FG=8,BF+CG=BH=6,从而求出面积和为24,是定值.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( ) 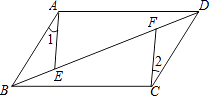
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批零件共有3000件,为了检查这批零件的质量,从中随机抽取一部分测量了它们的长度(单位:mm),并根据得到的数据,绘制出如下的统计图①和图②. 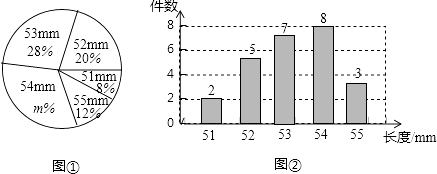
(1)本次随机抽取的零件的件数为 , 图①中m的值为;
(2)求本次随机抽取的零件长度的平均数、中位数和众数;
(3)根据样本数据,估计该批零件中长度为52mm的零件件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,求CD的长. 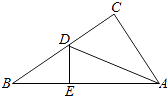
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出四个命题:①若a>b,c=d,则ac>bd;②若ac>bc,则a>b;③若a>b,则ac2>bc2;④若ac2>bc2,则a>b.正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
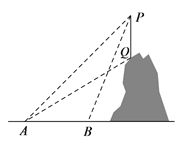
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com