
【题目】如图所示,在平面直角坐标系中,一次函数y=ax+1(a≠0)与反比例函数y=![]() (k≠0)的图象交于A、D两点,AB⊥x轴于点B,tan∠AOB=
(k≠0)的图象交于A、D两点,AB⊥x轴于点B,tan∠AOB=![]() ,OB=2.
,OB=2.
(1)求反比例函数和一次函数的解析式;
(2)求△AOD的面积.
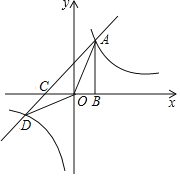
【答案】(1)反比例函数的解析式是:y=![]() ,一次函数的解析式是:y=x+1;(2)
,一次函数的解析式是:y=x+1;(2)![]() .
.
【解析】
(1)求出A的坐标,代入两函数的解析式,求出即可;
(2)求出两函数的解析式组成的方程组,求出方程组的解,即可得出D的坐标,求出C的坐标,根据三角形的面积公式求出即可.
解:(1)∵tan∠AOB=![]() =
=![]() ,OB=2,
,OB=2,
∴设AB=3,
∴A的坐标是(2,3),
把A的坐标代入y=![]() 得:k=6,
得:k=6,
∴反比例函数的解析式是:y=![]() ,
,
把A的坐标代入y=ax+1得:3=2a+1得:a=1,
∴一次函数的解析式是:y=x+1;
(2)解方程组 ,得:
,得:![]() 或
或![]() ,
,
∵A(2,3),
∴D(﹣3,﹣2).
把y=0代入y=x+1得:0=x+1,解得x=﹣1,
∴OC=1,
∴S△AOD=S△AOC+S△DOC
=![]() ×1×3+
×1×3+![]() ×1×2
×1×2
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
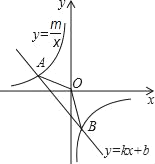
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(12,0),B(0,9)分别是平面直解坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交与点P、Q,则线段PQ长度的最小值是( )
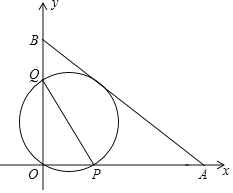
A.![]() B.10C.7.2D.
B.10C.7.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
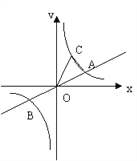
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于A、B两点,点B坐标为(-4,-2),C为双曲线
交于A、B两点,点B坐标为(-4,-2),C为双曲线![]() 上一点,且在第一象限内,若△AOC面积为6,则点C坐标为( )
上一点,且在第一象限内,若△AOC面积为6,则点C坐标为( )
A. (4,2) B. (2,3) C. (3,4) D. (2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个三角形不一定相似的是
A.两条直角边的比都是![]() 的两个直角三角形
的两个直角三角形
B.腰与底的比都是![]() 的两个等腰三角形
的两个等腰三角形
C.有一个内角为![]() 的两个直角三角形
的两个直角三角形
D.有一个内角为![]() 的两个等腰三角形
的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+1)x+4(k﹣![]() )=0.
)=0.
(1)求证:无论k取何值,此方程总有实数根;
(2)若等腰△ABC的一边长a=3,另两边b、c恰好是这个方程的两个根,求k值多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com