
【题目】如图,A(12,0),B(0,9)分别是平面直解坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交与点P、Q,则线段PQ长度的最小值是( )
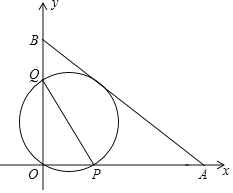
A.![]() B.10C.7.2D.
B.10C.7.2D.![]()
【答案】C
【解析】
设QP的中点为F,圆F与AB的切点为D,连接FD,连接OF,OD,则有FD⊥AB;由勾股定理的逆定理知,△ABO是直角三角形,FO+FD=PQ,由三角形的三边关系知,FO+FD≥OD;只有当点F、O、D共线时,FO+FD=PQ有最小值,最小值为OD的长,即当点F在直角三角形ABO的斜边AB的高OD上时,PQ=OD有最小值,由直角三角形的面积公式知,此时OD=![]() =
=![]() =7.2.
=7.2.
解:如图,设QP的中点为F,圆F与AB的切点为D,连接FD、OF、OD,则FD⊥AB.
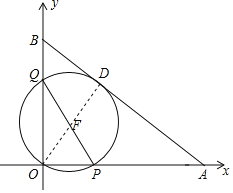
∵A(12,0)、B(0,9),
∴AO=12,BO=9,
∴AB=15,
∴∠AOB=90°,
∴PQ是圆F的直径,
∴FO+FD=PQ,
∴FO+FD≥OD,
当点F、O、D共线时,PQ有最小值,此时PQ=OD,
∴OD=![]() =
=![]() =7.2.
=7.2.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
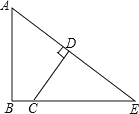
(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
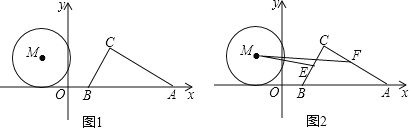
【题目】如图1,有一块直角三角板,其中![]() ,
,![]() ,
,![]() ,A、B在x轴上,点A的坐标为
,A、B在x轴上,点A的坐标为![]() ,圆M的半径为
,圆M的半径为![]() ,圆心M的坐标为
,圆心M的坐标为![]() ,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒;
,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒;
![]() 求点C的坐标;
求点C的坐标;
![]() 当点M在
当点M在![]() 的内部且
的内部且![]() 与直线BC相切时,求t的值;
与直线BC相切时,求t的值;
![]() 如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使
如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使![]() ?若存在,直接写出t的值,若不存在,请说明理由.
?若存在,直接写出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
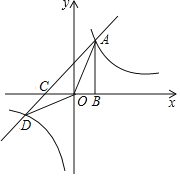
【题目】如图所示,在平面直角坐标系中,一次函数y=ax+1(a≠0)与反比例函数y=![]() (k≠0)的图象交于A、D两点,AB⊥x轴于点B,tan∠AOB=
(k≠0)的图象交于A、D两点,AB⊥x轴于点B,tan∠AOB=![]() ,OB=2.
,OB=2.
(1)求反比例函数和一次函数的解析式;
(2)求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y1=x2+bx+c与直线y2=﹣2x+m相交于A(﹣2,n)、B(2,﹣3)两点.
(1)求这条抛物线的解析式;
(2)若点D为抛物线的顶点,求三角形ABD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com