2015年十一国庆长假提前到9月29日，黄金周期间外出旅游更为火爆，若旅游区的门票为60元/张，某旅游区的开放时间为每天10小时，并每小时对进入旅游区的游客人数进行一次统计，下表是9月30日对进入旅游区人数的7次抽样统计数据：
| 记数的次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
| 每小时进入旅游区的人数 | 318 | 310 | 310 | 286 | 280 | 312 | 284 |
那么从9月29日至10月5日旅游区门票收入是多少？（ ）
A．900000元 B．129600元 C．191600元 D．162000元
科目：初中数学 来源： 题型：
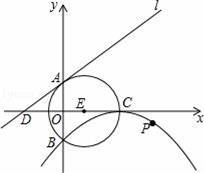
如图，⊙E的圆心E（3，0），半径为5，⊙E与y轴相交于A、B两点（点A在点B的上方），与x轴的正半轴交于点C，直线l的解析式为y=
x+4，与x轴相交于点D，以点C为顶点的抛物线过点B．
（1）求抛物线的解析式；
（2）判断直线l与⊙E的位置关系，并说明理由；
（3）动点P在抛物线上，当点P到直线l的距离最小时．求出点P的坐标及最小距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
已知抛物线y=x2﹣（4m+1）x+2m﹣1与x轴交于两点，如果有一个交点的横坐标大于2，另一个交点的横坐标小于2，并且抛物线与y轴的交点在点（0，
）的下方，那么m的取值范围是（ ）
A．
B．
C．
D．全体实数
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，四边形ABCD是菱形，对角线AC与BD交于点O，且AC=80，BD=60．动点M、N分别以每秒1个单位的速度从点A、D同时出发，分别沿A→O→D和D→A运动，当点N到达点A时，M、N同时停止运动．设运动时间为t秒．
（1）求菱形ABCD的周长；
（2）记△DMN的面积为S，求S关于t的解析式，并求S的最大值；
（3）当t=30秒时，在线段OD的垂直平分线上是否存在点P，使得∠DPO=∠DON？若存在，这样的点P有几个？并求出点P到线段OD的距离；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
在平面直角坐标系中，点O为坐标原点，A、B、C三点的坐标分别为A（2，0），B（4，0），C（0，5），点D在第一象限内，且∠ADB=45°．线段CD的长的最小值为
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD于F．
（1）求证：①△AEF≌△BEC；②四边形BCFD是平行四边形；
（2）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，求sin∠ACH的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，半径为2cm，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为（ ）
A．（
﹣1）cm2 B．（ +1）cm2 C．1cm2 D． cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=300（人）；
，则
=